Trong mặt phẳng Oxy, cho hai điểm A(–3; 0), B(1; –2) và đường thẳng d: x + y – 1 = 0

Trong mặt phẳng Oxy, cho hai điểm A(–3; 0), B(1; –2) và đường thẳng d: x + y – 1 = 0.

Sách bài tập Toán 10 Kết nối tri thức Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Bài 7.17 trang 38 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho hai điểm A(–3; 0), B(1; –2) và đường thẳng d: x + y – 1 = 0.

a) Chứng minh rằng hai điểm A và B nằm cùng phía so với đường thẳng d.

b) Điểm M thay đổi trên đường thẳng d. Tìm giá trị nhỏ nhất của chu vi tam giác ABM.

Lời giải:

a)

Ta có (–3 + 0 – 1).(1 – 2 – 1) = 8 > 0 nên theo tập nghiệm của bất phương trình bậc nhất hai ẩn ta có A, B nằm cùng phía so với đường thẳng d.

b)

Dựa vào phương trình đường thẳng d ta có:

x + y – 1 = 0

⇔ y = 1 – x

Do M thuộc đường thẳng d nên toạ độ của điểm M có dạng M(t; 1– t).

Chu vi tam giác ABM là: AB + MA + MB

Mà AB luôn không đổi nên chu vi tam giác ABM nhỏ nhất khi và chỉ khi MA + MB nhỏ nhất.

Lấy A’ đối xứng với A qua đường thẳng d. Khi đó ta có:

MA + MB = MA’ + MB ≥ A’B

Dấu bằng xảy ra khi M = A’B ∩ d

Gọi H là hình chiếu vuông góc của A lên d. Khi đó AH đi qua điểm A(–3;0) và nhận vectơ chỉ phương $\overrightarrow{u_d}=\left(1;-1\right)$ của đường thẳng d là vectơ pháp tuyến nên phương trình của AH là:

1(x + 3) – 1(y – 0) = 0

⇔ x – y + 3 = 0

Vậy toạ độ điểm H là nghiệm của hệ phương trình

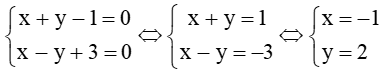
Suy ra H(–1; 2). Mặt khác, H là trung điểm của AA’ nên ta có:

x_H = (x_A + x_A’) : 2 ⇔ x_{A’ ­­­­­­}= 2x_H – x_A = 2.(–1) – (–3) = 1

y_H = (y_A + y_A’) : 2 ⇔ y_{A’ ­­­­­­}= 2y_H – y_A = 2.2 – 0 = 4

Do đó, ta có A’(1; 4)

Ta có $\overrightarrow{A\text{'}B}=\left(0;-6\right)$ là một vectơ chỉ phương của đường thẳng A’B. Do đó A’B là đường thẳng đi qua đểm A’(1; 4) và nhận $\overrightarrow{n}=\left(1;0\right)$ là một vectơ pháp tuyến. Phương trình của đường thẳng A’B là:

1(x – 1) + 0(y – 4) = 0

⇔ x – 1 = 0

Vậy toạ độ điểm M là nghiệm của hệ phương trình

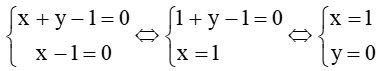
Do đó ta có M(1; 0).