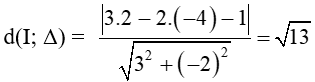Viết phương trình của đường tròn (C) trong các trường hợp sau

Viết phương trình của đường tròn (C) trong các trường hợp sau.

Sách bài tập Toán 10 Kết nối tri thức Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài 7.21 trang 41 Sách bài tập Toán lớp 10 Tập 2: Viết phương trình của đường tròn (C) trong các trường hợp sau.

a) Có tâm I(3; 1) và có bán kính R = 2.

b) Có tâm I(3; 1) và đi qua điểm M(–1; 7).

c) Có tâm I(2; –4) và tiếp xúc với đường thẳng Δ: 3x – 2y – 1 = 0.

d) Có đường kính AB với A(4; 1), B(–2; –5).

Lời giải:

a)

Phương trình đường tròn có tâm I(3; 1) và có bán kính R = 2 là:

(x – 3)² + (y – 1)² = 2²

⇔ (x – 3)² + (y – 1)² = 4.

b)

Đường tròn có tâm I(3; 1) và đi qua điểm M(–1; 7) có bán kính

R = IM = $\sqrt{{(-1-3)}^2+{(7-1)}^2}=2\sqrt{13}$

Phương trình đường tròn có tâm I(3; 1) và đi qua điểm M(–1; 7) là:

(x – 3)² + (y – 1)² = ($2\sqrt{13}$)²

⇔ (x – 3)² + (y – 1)² = 52.

c)

Đường tròn có tâm I(2; –4) và tiếp xúc với đường thẳng Δ: 3x – 2y – 1 = 0 có bán kính R =

Phương trình đường tròn có tâm I(2; –4) và tiếp xúc với đường thẳng Δ: 3x – 2y – 1 = 0 là:

(x – 2)² + (y + 4)² = ($\sqrt{13}$)²

⇔ (x – 2)² + (y + 4)² = 13.

d)

Đường tròn có đường kính AB với A(4; 1), B(–2; –5) có:

Tâm I là trung điểm AB nên:

x_I = (x_A + x_B) : 2 = (4 + (– 2)) : 2 = 1

y_I = (y_A + y_B) : 2 = (1 + (– 5)) : 2 = –2

Do đó, I(1; –2).

Bán kính R = $\frac{AB}{2}=\frac{\sqrt{{(-2-4)}^2+{(-5-1)}^2}}{2}=3\sqrt{2}$

Phương trình đường tròn có đường kính AB với A(4; 1), B(–2; –5) là:

(x – 1)² + (y + 2)² = ($3\sqrt{2}$)²

⇔ (x – 1)² + (y + 2)² = 18.