Cho điểm A(4; 2) và hai đường thẳng d: 3x + 4y – 20 = 0, d’: 2x + y = 0

Cho điểm A(4; 2) và hai đường thẳng d: 3x + 4y – 20 = 0, d’: 2x + y = 0.

Sách bài tập Toán 10 Kết nối tri thức Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài 7.24 trang 42 Sách bài tập Toán lớp 10 Tập 2: Cho điểm A(4; 2) và hai đường thẳng d: 3x + 4y – 20 = 0, d’: 2x + y = 0.

a) Viết phương trình đường thẳng Δ đi qua A và vuông góc với d.

b) Viết phương trình đường tròn (C) có tâm thuộc đường thẳng d' và tiếp xúc với d tại điểm A.

Lời giải:

a)

Dựa vào đề bài ta có do đường thẳng Δ vuông góc với d nên: $\overrightarrow{u_{∆}}=\overrightarrow{n_d}=\left(3;4\right)\Rightarrow \overrightarrow{n_{∆}}=\left(4;-3\right)$.

Phương trình của Δ là:

4(x – 4) – 3(y – 2) = 0

⇔ 4x – 3y – 10 = 0.

b)

Gọi I là tâm của đường tròn (C).

Vì d tiếp xúc với (C) tại điểm A nên ta có IA ⊥ d, do đó I thuộc Δ. Mặt khác, I thuộc đường thẳng d'. Suy ra toạ độ của I thoả mãn hệ phương trình

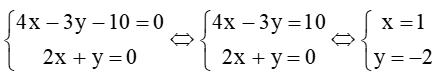
Do đó, I(1; –2)

Bán kính của (C) là: $R=IA=\sqrt{{(4-1)}^2+(2-{(-2))}^2}=5$

Vậy phương trình của (C) là

(x – 1)² + (y + 2)² = 5²

⟺ (x – 1)² + (y + 2)² = 25.