Cho đường thẳng Δ: x . sinα° + y . cosα° – 1 = 0, trong đó α là một số thực

Cho đường thẳng Δ: x . sinα° + y . cosα° – 1 = 0, trong đó α là một số thực thuộc khoảng (0; 180).

Sách bài tập Toán 10 Kết nối tri thức Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài 7.26 trang 42 Sách bài tập Toán lớp 10 Tập 2: Cho đường thẳng Δ: x . sinα° + y . cosα° – 1 = 0, trong đó α là một số thực thuộc khoảng (0; 180).

a) Tính khoảng cách từ gốc toạ độ O đến đường thẳng Δ.

b) Chứng minh rằng khi α thay đổi, tồn tại một đường tròn cố định luôn tiếp xúc với đường thẳng Δ.

Lời giải:

a)

Khoảng cách từ O(0; 0) đến đường thẳng Δ là

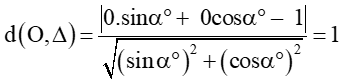
Do (sinα^o)² + (cosα^o)² = 1 với α là một số thực thuộc khoảng (0; 180).

b)

Giả sử (C) là đường tròn có tâm O và bán kính R = 1.

Với α là một số thực thuộc khoảng (0; 180) có thể thay đổi thì có:

d(O, Δ) = 1 = R không đổi

nên (C) luôn tiếp xúc với Δ.

Vậy phương trình đường tròn (C) cần tìm là x² + y² = 1.