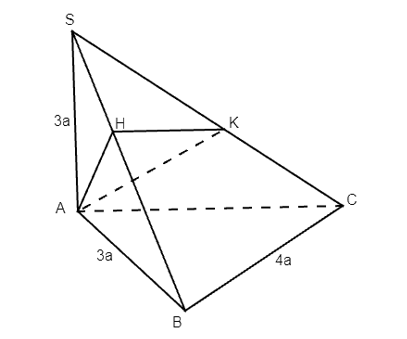
Cho hình chóp S.ABC có SA ⊥ (ABC), AB ⊥ BC, SA = AB = 3a, BC = 4a

❮ Bài trước Bài sau ❯

Cho hình chóp S.ABC có SA ⊥ (ABC), AB ⊥ BC, SA = AB = 3a, BC = 4a. Gọi α, β, γ lần lượt là số đo của các góc nhị diện [B, SA, C], [A, BC, S], [A, SC, B]. Tính:

Giải sách bài tập Toán 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 27 trang 99 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC), AB ⊥ BC, SA = AB = 3a, BC = 4a. Gọi α, β, γ lần lượt là số đo của các góc nhị diện [B, SA, C], [A, BC, S], [A, SC, B]. Tính:

a) cosα, cosβ;

b*) cosγ.

Lời giải:

Cho hình chóp S.ABC có SA ⊥ (ABC), AB ⊥ BC, SA = AB = 3a, BC = 4a

a) Do SA ⊥ (ABC) nên SA ⊥ AB, SA ⊥ AC và SA ⊥ BC.

· Ta có: AB ⊥ SA, AC ⊥ SA và AB ∩ AC = A ∈ SA.

Suy ra $\hat{B A C}$ chính là góc phẳng nhị diện của góc nhị diện [B, SA, C], tức là $α = \hat{B A C} .$

Xét tam giác ABC vuông tại B có:

AC² = AB² + BC² ⇒ AC² = (3a)² + (4a)² = 25a²⇒ AC = 5a.

Và $\cos α = \cos \hat{B A C} = \frac{A B}{A C} = \frac{3 a}{5 a} = \frac{3}{5} .$

· Ta có: BC ⊥ SA, BC ⊥ AB và SA ∩ AB = A trong (SAB) suy ra BC ⊥ (SAB).

Mà SB ⊂ (SBC) nên BC ⊥ SB.

Ta có: AB ⊥ BC, SB ⊥ BC và AB ∩ SB = B ∈ BC.

Suy ra $\hat{S B A}$ chính là góc phẳng nhị diện của góc nhị diện [A, BC, S], tức là $β = \hat{S B A} .$

Xét tam giác SAB vuông tại A có:

SB² = SA² + AB² ⇒ SB² = (3a)² + (3a)² = 18a² $\Rightarrow S B = 3 \sqrt{2} a .$

Và $\cos β = \cos \hat{S B A} = \frac{A B}{S B} = \frac{3 a}{3 \sqrt{2} a} = \frac{\sqrt{2}}{2} .$

b*) Gọi H và K lần lượt là hình chiếu của A trên SB và SC nên AH ⊥ SB và AK ⊥ SC.

Do BC ⊥ (SAB) (cmt) và AH ⊂ (SAB) nên BC ⊥ AH.

Ta có: AH ⊥ SB, AH ⊥ BC và SB ∩ BC = B trong (SBC) nên AH ⊥ (SBC).

Mà SC ⊂ (SBC) và HK ⊂ (SBC).

Suy ra: AH ⊥ SC và AH ⊥ HK.

Ta có: SC ⊥ AH, SC ⊥ AK (cmt) và AH ∩ AK = A trong (AHK) nên SC ⊥ (AHK).

Mà HK ⊂ (AHK).

Suy ra SC ⊥ HK.

Từ đó ta có: HK ⊥ SC, AK ⊥ SC và HK ∩ AK = K ∈ SC.

Suy ra $\hat{A K H}$ chính là góc phẳng nhị diện của góc nhị diện [A, SC, B], tức là $γ = \hat{A K H} .$

Áp dụng hệ thức lượng trong:

· Tam giác SAB vuông tại A với đường cao AH có:

AH. SB = SA. AB $\Rightarrow A H = \frac{S A . A B}{S B} = \frac{3 a .3 a}{3 \sqrt{2} a} = \frac{3}{\sqrt{2}} a .$

· Tam giác SAC vuông tại A với đường cao AK có:

AK. SC = SA. AC $\Rightarrow A K = \frac{S A . A C}{S C} = \frac{S A . A C}{\sqrt{S A^{2} + A C^{2}}}$

(Do tam giác SAC vuông tại A nên $S C = \sqrt{S A^{2} + A C^{2}}$ )

$\Rightarrow A K = \frac{3 a .5 a}{\sqrt{{(3 a)}^{2} + {(5 a)}^{2}}} = \frac{15 a^{2}}{a \sqrt{34}} = \frac{15 a}{\sqrt{34}} .$

Xét tam giác AHK vuông tại H (vì AH ⊥ HK) có:

$H K = \sqrt{A K^{2} - A H^{2}} = \sqrt{{(\frac{15 a}{\sqrt{34}})}^{2} - {(\frac{3 a}{\sqrt{2}})}^{2}} = \frac{6 a}{\sqrt{17}} .$

Và $\cos γ = \cos \hat{A K H} = \frac{H K}{A K} = \frac{\frac{6 a}{\sqrt{17}}}{\frac{15 a}{\sqrt{34}}} = \frac{2 \sqrt{2}}{5} .$

Lời giải SBT Toán 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện hay khác:

Xem thêm lời giải Sách bài tập Toán 11 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯