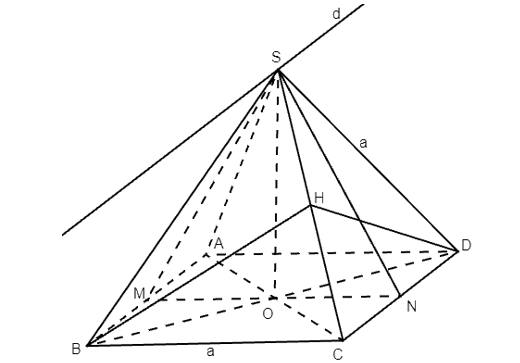
Cho hình chóp S.ABCD có ABCD là hình vuông, AC cắt BD tại O, SO ⊥ (ABCD)

Cho hình chóp S.ABCD có ABCD là hình vuông, AC cắt BD tại O, SO ⊥ (ABCD). Tất cả các cạnh của hình chóp bằng a.

Giải sách bài tập Toán 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 28 trang 100 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có ABCD là hình vuông, AC cắt BD tại O, SO ⊥ (ABCD). Tất cả các cạnh của hình chóp bằng a.

a) Tính góc giữa đường thẳng SB và mặt phẳng (SAC).

b) Gọi α là số đo của góc nhị diện [S, CD, A]. Tính cosα.

c) Gọi d là giao tuyến giữa hai mặt phẳng (SAB) và (SCD), β là số đo của góc nhị diện [A, d, D]. Tính cosβ.

d*) Gọi γ là số đo góc nhị diện [B, SC, D]. Tính cosγ.

Lời giải:

Cho hình chóp S.ABCD có ABCD là hình vuông, AC cắt BD tại O, SO ⊥ (ABCD)

a) Ta có: SO ⊥ (ABCD) và OB ⊂ (ABCD) nên SO ⊥ OB.

Do ABCD là hình vuông nên OB ⊥ AC.

Ta có: OB ⊥ SO, OB ⊥ AC và SO ∩ AC = O trong (SAC) nên OB ⊥ (SAC) hay O là hình chiếu vuông góc của B trên (SAC).

Do đó góc giữa SB và (SAC) là góc giữa SB và SO và bằng $\hat{B S O}$ .

Vì ABCD là hình vuông cạnh a, nên $B D = A C = a \sqrt{2} .$

Xét tam giác SDB có: SB = SD = a và SB² + SD² = a² + a² = 2a² = BD² nên tam giác SBD vuông cân tại S.

Hơn nữa SO ⊥ BD (vì SO ⊥ (ABCD)).

Nên SO là đường phân giác của $\hat{B S D \Rightarrow \hat{B S O} = \hat{O S D} = \frac{90 °}{2} = 45 ° .}$

Vậy góc giữa đường thẳng SB và mặt phẳng (SAC) bằng 45°.

b) Gọi N là trung điểm của CD suy ra $C N = \frac{C D}{2} = \frac{a}{2} .$

Ta có: tam giác SCD đều (vì SC = SD = CD = a), SN là đường trung tuyến

Suy ra: SN ⊥ CD.

Áp dụng định lí Pythagore trong tam giác SNC vuông tại N có

SC² = CN² + SN²

Suy ra $S N = \sqrt{S C^{2} - C N^{2}} = \sqrt{a^{2} - {(\frac{a}{2})}^{2}} = \frac{a \sqrt{3}}{2} .$

Xét tam giác ACD có: O, N lần lượt là trung điểm của AC và DC nên ON là đường trung bình của tam giác ACD.

Suy ra: ON // AD và $O N = \frac{1}{2} A D = \frac{a}{2} .$

Mà AD ⊥ CD (vì ABCD là hình vuông)

Nên ON ⊥ CD.

Ta thấy: SN ⊥ CD, ON ⊥ CD và SN ∩ ON = N ∈ CD.

Suy ra $\hat{S N O}$ chính là góc phẳng nhị diện của góc nhị diện [S, CD, A], tức là $α = \hat{S N O} .$

Vì SO ⊥ (ABCD) và ON ⊂ (ABCD) nên SO ⊥ ON.

Xét tam giác SNO vuông tại O có:

$\cos \hat{S N O} = \frac{O N}{S N} = \frac{\frac{a}{2}}{\frac{a \sqrt{3}}{2}} = \frac{\sqrt{3}}{3} \Rightarrow \cos α = \frac{\sqrt{3}}{3} .$

c) Ta có: S ∈ (SAB) ∩ (SCD), AB // CD, AB ⊂ (SAB) và CD ⊂ (SCD)

Suy ra giao tuyến d của hai mặt phẳng (SAB) và (SCD) đi qua S và song song với AB và CD.

Gọi M là trung điểm của AB.

Tương tự câu b) ta có $S M = \frac{a \sqrt{3}}{2},$ $M O = \frac{a}{2}$ và $M N = M O + O N = \frac{a}{2} + \frac{a}{2} = a .$

Ta có: tam giác SAB đều (vì SA = SB = AB = a), SM là đường trung tuyến

Nên SM ⊥ AB mà AB // d suy ra SM ⊥ d.

Tương tự ta có: SN ⊥ CD mà CD // d suy ra SN ⊥ d.

Ta thấy: SM ⊥ d, SN ⊥ d và SM ∩ SN = S ∈ d và SM, SN lần lượt nằm trong mặt phẳng nhị diện chứa đường thẳng d và điểm A, mặt phẳng nhị diện chứa đường thẳng d và điểm D.

Suy ra $\hat{M S N}$ là góc phẳng nhị diện của góc nhị diện [A, d, D], tức là $β = \hat{M S N} .$

Áp dụng định lí Cosin trong tam giác SMN có:

$\cos \hat{M S N} = \frac{S M^{2} + S N^{2} - M N^{2}}{2 \cdot S M \cdot S N} .$

$\Rightarrow \cos β = \cos \hat{M S N} = \frac{{(\frac{a \sqrt{3}}{2})}^{2} + {(\frac{a \sqrt{3}}{2})}^{2} - a^{2}}{2 \cdot \frac{a \sqrt{3}}{2} \cdot \frac{a \sqrt{3}}{2}} = \frac{1}{3} .$

d) Gọi H là hình chiếu của B trên SC nên BH ⊥ SC.

Ta có OB ⊥ (SAC) hay BD ⊥ (SAC).

Mà SC ⊂ (SAC) nên BD ⊥ SC.

Ta có: SC ⊥ BH, SC ⊥ BD và BH ∩ BD = B trong (BHD) nên SC ⊥ (BHD)

Mặt khác HD ⊂ (BHD) nên SC ⊥ HD.

Ta thấy: HD ⊥ SC, BH ⊥ SC và HD ∩ BH = H ∈ SC.

Suy ra $\hat{B H D}$ là góc phẳng nhị diện của góc nhị diện [B, SC, D], tức là $γ = \hat{B H D} .$

Xét tam giác SBC đều cạnh a (vì SB = SC = SD = BC = CD = a) có: BH ⊥ SC.

Nên BH là đường trung tuyến, suy ra $S H = \frac{S C}{2} = \frac{a}{2} .$

Áp dụng định lí Pythagore trong tam SBH vuông tại H có:

SB² = BH² + SH²

Suy ra $B H = \sqrt{S B^{2} - S H^{2}} = \sqrt{a^{2} - {(\frac{a}{2})}^{2}} = \frac{a \sqrt{3}}{2} .$

Tương tự: tam giác SCD đều và đường trung tuyến $H D = \frac{a \sqrt{3}}{2} .$

Áp dụng định lí Cosin trong tam giác BHD có:

$\cos γ = \cos \hat{B H D} = \frac{H B^{2} + H D^{2} - B D^{2}}{2 H B . H D} .$

$\Rightarrow \cos γ = \frac{{(\frac{a \sqrt{3}}{2})}^{2} + {(\frac{a \sqrt{3}}{2})}^{2} - {(a \sqrt{2})}^{2}}{2. \frac{a \sqrt{3}}{2} . \frac{a \sqrt{3}}{2}} = - \frac{1}{3} .$

Lời giải SBT Toán 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện hay khác:

Xem thêm lời giải Sách bài tập Toán 11 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯