Cho hình chóp S.ABCD có SA ⊥ (ABCD), ABCD là hình thoi cạnh a

Cho hình chóp S.ABCD có SA ⊥ (ABCD), ABCD là hình thoi cạnh a, AC = a, Tính số đo của góc nhị diện [S, CD, A].

Giải sách bài tập Toán 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 29 trang 100 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD), ABCD là hình thoi cạnh a, AC = a, $S A = \frac{a}{2} .$ Tính số đo của góc nhị diện [S, CD, A].

Lời giải:

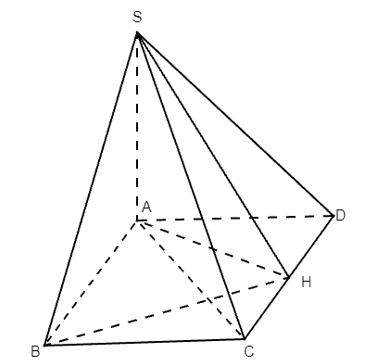
Gọi H là hình chiếu của A trên CD suy ra AH ⊥ CD.

Ta có: SA ⊥ (ABCD), CD ⊂ (ABCD) và AH ⊂ (ABCD).

Suy ra: SA ⊥ CD và SA ⊥ AH.

Ta có: CD ⊥ AH, CD ⊥ SA và AH ∩ SA = A trong (SAH) nên CD ⊥ (SAH).

Mà SH ⊂ (SAH), suy ra CD ⊥ SH.

Ta thấy: SH ⊥ CD, AH ⊥ CD và SH ∩ AH = H ∈ CD.

Suy ra $\hat{S H A}$ là góc phẳng nhị diện của góc nhị diện [S, CD, A].

Vì AD = CD = AC = a nên tam giác ACD đều.

Hơn nữa, AH là đường cao của tam giác ACD (do AH ⊥ CD) nên AH cũng là đường đường trung tuyến của tam giác ACD.

Suy ra $H D = \frac{A D}{2} = \frac{a}{2} .$

Áp dụng định lí Pythagore trong tam giác AHD vuông tại H có:

AD² = AH² + HD²

Suy ra $A H = \sqrt{A D^{2} - H D^{2}} = \sqrt{a^{2} - {(\frac{a}{2})}^{2}} = \frac{a \sqrt{3}}{2} .$

Xét tam giác SAH vuông tại A có:

$\tan \hat{S H A} = \frac{S A}{A H} = \frac{\frac{a}{2}}{\frac{a \sqrt{3}}{2}} = \frac{\sqrt{3}}{3} \Rightarrow \hat{S H A} = 30 ° .$

Vậy số đo của góc nhị diện [S, CD, A] là $\hat{S H A} = 30 ° .$

Lời giải SBT Toán 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện hay khác:

Xem thêm lời giải Sách bài tập Toán 11 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯