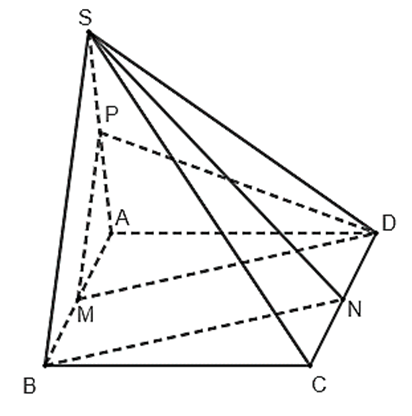
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm các cạnh AB, CD, SA
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm các cạnh AB, CD, SA. Khẳng định nào sau đây là đúng?
Giải SBT Toán 11 Cánh diều Bài 4: Hai mặt phẳng song song
Bài 30 trang 108 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm các cạnh AB, CD, SA. Khẳng định nào sau đây là đúng?
A. (SBN) // (DAP).
B. (SBC) // (MPD).
C. (SBN) // (PMD).
D. (SDN) // (MAP).
Lời giải:
Đáp án đúng là: C
+ Ta có, P ∈ SA nên mặt phẳng (DAP) chính là mặt phẳng (SAD).
Mà hai mặt phẳng (SAD) và (SBN) có điểm chung là S nên chúng không thể song song.
Vậy hai mặt phẳng (SBN) và (DAP) không song song với nhau.
Do đó, đáp án A sai.
+ Trong mặt phẳng (ABCD), hai đường thẳng MD và BC cắt nhau.
Vậy hai mặt phẳng (SBC) và (MPD) không thể song song.
Do đó, đáp án B sai.
+ Mặt phẳng (MAP) chính là mặt phẳng (SAB).
Hai mặt phẳng (SAB) và (SDN) có điểm chung là S.
Vậy hai mặt phẳng (MAP) và (SAB) không thể song song.
Do đó, đáp án D sai. Vậy đáp án C đúng. Ta chứng minh như sau:
+ Vì M, N lần lượt là trung điểm của AB, CD và AB = CD, AB // CD (do ABCD là hình bình hành) nên BM // ND và BM // ND. Do đó, BMDN là hình bình hành.
Suy ra MD // BN. Mà BN ⊂ (SBN) nên MD // (SBN).
Lại có MP là đường trung bình của tam giác SAB nên MP // SB.
Mà SB ⊂ (SBN) nên MP // (SBN).
Vì MD và MP cắt nhau trong mặt phẳng (MPD) nên (MPD) // (SBN).
Lời giải Sách bài tập Toán lớp 11 Bài 4: Hai mặt phẳng song song hay khác: