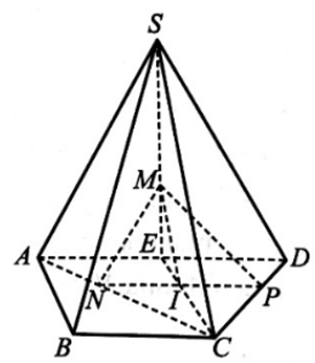
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD. Gọi M là trọng tâm của tam giác SAD, N là điểm thuộc đoạn thẳng AC sao cho AN = AC, P là điểm thuộc đoạn thẳng CD sao cho DP = DC. Chứng minh rằng (MNP) // (SBC).
Giải SBT Toán 11 Cánh diều Bài 4: Hai mặt phẳng song song
Bài 34 trang 108 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD. Gọi M là trọng tâm của tam giác SAD, N là điểm thuộc đoạn thẳng AC sao cho AN = AC, P là điểm thuộc đoạn thẳng CD sao cho DP = DC. Chứng minh rằng (MNP) // (SBC).
Lời giải:
Gọi E là trung điểm của AD và I là giao điểm của NP và EC.
Ta có nên NP // AD.
Do AD // BC (ABCD là hình thang có AD là đáy) nên NP // BC.
Mà BC ⊂ (SBC). Suy ra NP // (SBC). (1)
Vì NP // AD nên ta có .
Do M là trọng tâm của tam giác SAD và E trung điểm của đoạn AD nên M ∈ SE và .
Như vậy nên MI // SC.
Mà SC ⊂ (SBC). Suy ra MI // (SBC). (2)
Lại có MI và NP là hai đường thẳng cắt nhau tại I trong mặt phẳng (MNP). (3)
Từ (1), (2) và (3) suy ra (MNP) // (SBC).
Lời giải Sách bài tập Toán lớp 11 Bài 4: Hai mặt phẳng song song hay khác: