Cho hình lăng trụ ABC.A’B’C’ có AA’ ⊥ (ABC), tam giác ABC cân tại A
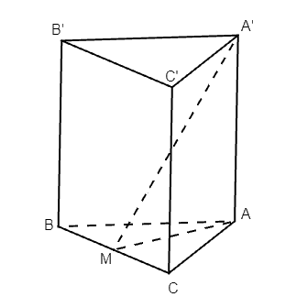
Cho hình lăng trụ ABC.A’B’C’ có AA’ ⊥ (ABC), tam giác ABC cân tại A. Gọi M là trung điểm của BC. Chứng minh rằng (MAA’) ⊥ (BCC’B’).
Giải sách bài tập Toán 11 Bài 4: Hai mặt phẳng vuông góc
Bài 39 trang 104 SBT Toán 11 Tập 2: Cho hình lăng trụ ABC.A’B’C’ có AA’ ⊥ (ABC), tam giác ABC cân tại A. Gọi M là trung điểm của BC. Chứng minh rằng (MAA’) ⊥ (BCC’B’).
Lời giải:
Vì tam giác ABC cân tại A, AM là đường trung tuyến nên AM ⊥ BC.
Ta có: AA’ ⊥ (ABC), AA’ // BB’, suy ra BB’ ⊥ (ABC).
Mà AM ⊂ (ABC) nên BB’ ⊥ AM.
Ta có: AM ⊥ BC, AM ⊥ BB’, BC ∩ BB’ = B trong (BCC’B’).
Từ đó suy ra AM ⊥ (BCC’B’).
Mà AM ⊂ (MAA’) nên (MAA’) ⊥ (BCC’B’).
Lời giải SBT Toán 11 Bài 4: Hai mặt phẳng vuông góc hay khác: