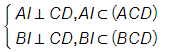Cho tứ diện ABCD có tam giác BCD vuông cân tại B và AB ⊥ (BCD)

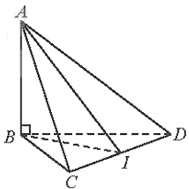
Cho tứ diện ABCD có tam giác BCD vuông cân tại B và AB ⊥ (BCD). Cho biết BC = , AB = . Xác định và tính góc giữa hai mặt phẳng (ACD) và (BCD).

Giải sách bài tập Toán 11 Bài 3: Hai mặt phẳng vuông góc - Chân trời sáng tạo

Bài 1 trang 61 SBT Toán 11 Tập 2: Cho tứ diện ABCD có tam giác BCD vuông cân tại B và AB ⊥ (BCD). Cho biết BC = $a\sqrt{2}$ , AB = $\frac{a}{\sqrt{3}}$. Xác định và tính góc giữa hai mặt phẳng (ACD) và (BCD).

Lời giải:

Gọi I là trung điểm của CD.

Ta có: CD ⊥ BI và CD ⊥ AB suy ra CD ⊥ AI.

Ta nhận thấy: CD là giao tuyến của 2 mặt phẳng (ACD) và (BCD);

Mà

Suy ra $\left(\right(ACD),(BCD\left)\right)=(AI,BI)=\widehat{AIB}.$

Tam giác BCD vuông cân tại B nên $BI=\frac{1}{2}CD=\frac{1}{2}.BC.\sqrt{2}=a.$

Xét tam giác ABI vuông tại B, ta có: 

$\tan \widehat{AIB}=\frac{AB}{BI}=\frac{1}{\sqrt{3}}\Rightarrow \widehat{AIB}=30°.$

Vậy góc giữa hai mặt phẳng (ACD) và (BCD) là  $\widehat{AIB}=30°$ .

Lời giải SBT Toán 11 Bài 3: Hai mặt phẳng vuông góc hay khác:

• Bài 2 trang 61 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a. Cho biết SA = a và SA ⊥ (ABCD). Trên BC lấy điểm I ....

• Bài 3 trang 61 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và SA ⊥ (ABC). ....

• Bài 4 trang 61 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). ....

• Bài 5 trang 62 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = $a\sqrt{3}$ . Hai mặt phẳng (SAB) và (SAD) ....

• Bài 6 trang 62 SBT Toán 11 Tập 2: Người ta cần sơn tất cả các mặt của một khối bê tông hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 2 m, đáy nhỏ có ....

• Bài 7 trang 62 SBT Toán 11 Tập 2: Một hộp đèn treo trần có hình dạng lăng trụ đứng lục giác đều (Hình 15), cạnh đáy bằng 10 cm và cạnh bên bằng 50 cm. ....