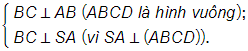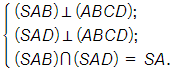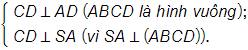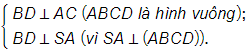Cho hình chóp S ABCD có đáy ABCD là hình vuông tâm O Hai mặt phẳng SAB và SAD
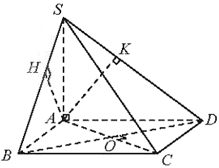
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi H và K lần lượt là hình chiếu của A trên SB và SD. Chứng minh rằng:
Giải sách bài tập Toán 11 Bài 3: Hai mặt phẳng vuông góc - Chân trời sáng tạo
Bài 4 trang 61 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi H và K lần lượt là hình chiếu của A trên SB và SD. Chứng minh rằng:
a) (SBC) ⊥ (SAB);
b) (SCD) ⊥ (SAD);
c) (SBD) ⊥ (SAC);
d) (SAC) ⊥ (AHK).
Lời giải:
a)Theo giả thiết:
Suy ra SA ⊥ (ABCD).
Khi đó:
BC ⊥ (SAB) (SBC) ⊥ (SAB).
b)Theo giả thiết:
Suy ra SA ⊥ (ABCD).
Khi đó:
CD ⊥ (SAD) (SCD) ⊥ (SAD).
c)Ta có:
BD ⊥ (SAC) (SBD) ⊥ (SAC).
d)Ta có:
(SAB) ⊥ (SBC) (Chứng minh trên);
(SAB) (SBC) = SB;
Do đó AH ⊥ (SBC)
Mà AH ⊥ SB (giả thiết).
Nên AH ⊥ SC. (1)
Tương tự: AK ⊥ SC. (2)
Từ (1) và (2) suy ra: SC ⊥ (AHK).
Vậy (SAC) ⊥ (AHK).
Lời giải SBT Toán 11 Bài 3: Hai mặt phẳng vuông góc hay khác: