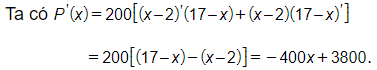Nếu số lượng sản phẩm sản xuất được của một nhà máy là x đơn vị trăm sản phẩm

Nếu số lượng sản phẩm sản xuất được của một nhà máy là x (đơn vị: trăm sản phẩm) thì lợi nhuận sinh ra là P(x) = 200(x – 2)(17 – x) (nghìn đồng). Tính tốc độ thay đổi lợi nhuận của nhà máy đó khi sản xuất 3000 sản phẩm

Giải sách bài tập Toán 11 Bài 2: Các quy tắc tính đạo hàm - Chân trời sáng tạo

Bài 8 trang 44 SBT Toán 11 Tập 2: Nếu số lượng sản phẩm sản xuất được của một nhà máy là x (đơn vị: trăm sản phẩm) thì lợi nhuận sinh ra là P(x) = 200(x – 2)(17 – x) (nghìn đồng). Tính tốc độ thay đổi lợi nhuận của nhà máy đó khi sản xuất 3000 sản phẩm

Lời giải:

$P^{\text{'}}\left(30\right)=\left(-400\right).30+3800=-8200$

Vậy tốc độ thay đổi lợi nhuận của nhà máy đó khi sản xuất 3000 sản phẩm là –8200 nghìn đồng.

Lời giải SBT Toán 11 Bài 2: Các quy tắc tính đạo hàm hay khác:

• Bài 1 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau: a) $y=\frac{-3x^2}{2}+\frac{2}{x}+\frac{x^3}{3}$; b) y = (x² − 1)(x² – 4)(x² + 9); c) $y=\frac{x^2-2x}{x^2+x+1}$; d) $y=\frac{1-2x}{x+1}$; ....

• Bài 2 trang 43 SBT Toán 11 Tập 2: Cho hàm số $f\left(x\right)=3x^3-4\sqrt{x}$. Tính $f\left(4\right);f^{\text{'}}\left(4\right);f\left(a^2\right);f^{\text{'}}\left(a^2\right)$ (a là hằng số khác 0). ....

• Bài 3 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau: a) y = (1 + x²)²⁰; b) $y=\frac{2+x}{\sqrt{1-x}}$. ....

• Bài 4 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau: a) $y=\frac{x}{\sin x-\cos x}$; b) $y=\frac{\sin x}{x}$; c) $y=\sin x-\frac{1}{3}{\sin }^{3}x$; d) y = cos (2sinx). ....

• Bài 5 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm cấp 2 của các hàm số sau: a) y = xsin 2x; b) y = cos²x; c) y = x⁴ – 3x³ + x² − 1. ....

• Bài 6 trang 43 SBT Toán 11 Tập 2: Một chất điểm chuyển động thẳng có phương trình s = 100 + 2t – t² trong đó thời gian được tính bằng giây và s được tính bằng mét. ....

• Bài 7 trang 44 SBT Toán 11 Tập 2: Một chuyển động thẳng xác định bởi phương trình s(t) = −2t³ + 75t + 3, trong đó s tính bằng mét và t là thời gian tính bằng giây ....