Cho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AB, BC, CD
Cho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AB, BC, CD. Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP) trong các trường hợp sau:
Giải sách bài tập Toán 11 Bài 11: Hai đường thẳng song song - Kết nối tri thức
Bài 4.13 trang 59 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AB, BC, CD. Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP) trong các trường hợp sau:
a) Đường thẳng NP song song với đường thẳng BD;
b) Đường thẳng NP cắt đường thẳng BD.
Lời giải:
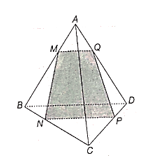
a)
Trong mặt phẳng (ABD), vẽ đường thẳng MQ // BD (Q ∈ AD).
Vì NP // BD nên MQ // NP, do đó Q thuộc mặt phẳng (MNP).
Vậy Q là giao điểm của đường thẳng AD và mặt phẳng (MNP).
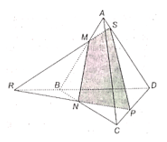
b)
Trong mặt phẳng (BCD), gọi R là giao điểm của NP và BD.
Trong mặt phẳng (ABD), gọi S là giao điểm của MR và AD.
Khi đó S là giao điểm của đường thẳng AD và mặt phẳng (MNP).
Lời giải SBT Toán 11 Bài 11: Hai đường thẳng song song hay khác: