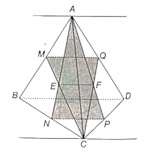
Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA
Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Giải sách bài tập Toán 11 Bài 11: Hai đường thẳng song song - Kết nối tri thức
Bài 4.16 trang 59 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Xác định giao tuyến của hai mặt phẳng (ANP) và (CMQ).
b) Xác định giao tuyến của hai mặt phẳng (ANP) và (ABD).
c) Xác định giao tuyến của hai mặt phẳng (CMQ) và (BCD).
d) Chứng minh rằng các giao tuyến tìm được ở trên đôi một song song với nhau.
Lời giải:
a) Trong mặt phẳng (ABC), gọi E là giao điểm của AN và CM.
Trong mặt phẳng (ACD), gọi F là giao điểm của AP và CQ.
Khi đó, đường thẳng EF là giao tuyến của hai mặt phẳng (ANP) và (CMQ).
b) Do E và F tương ứng là giao điểm của các đường trung tuyến trong tam giác ABC và tam giác ACD nên E và F lần lượt là trọng tâm của các tam giác này.
Suy ra , do đó EF // NP.
Lại có MQ và NP lần lượt là đường trung bình của tam giác ABD và tam giác CBD nên MQ // BD // NP.
Do vậy, EF // MQ // NP // BD.
Hai mặt phẳng (ANP) và (ABD) có điểm chung A và lần lượt chứa hai đường thẳng NP và BD song song với nhau nên giao tuyến của chúng là đường thẳng qua A và song song với BD.
c) Hai mặt phẳng (CMQ) và (BCD) có điểm chung C và lần lượt chứa hai đường thẳng MQ và BD song song với nhau nên giao tuyến của chúng là đường thẳng qua C và song song với BD.
d) Các giao tuyến đều song song với BD nên chúng đôi một song song với nhau.
Lời giải SBT Toán 11 Bài 11: Hai đường thẳng song song hay khác: