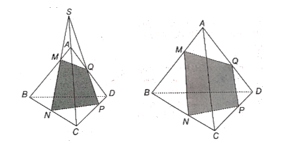
Cho tứ diện ABCD. Một mặt phẳng cắt bốn cạnh AB, BC, CD, DA lần lượt tại các điểm M, N, P, Q
Cho tứ diện ABCD. Một mặt phẳng cắt bốn cạnh AB, BC, CD, DA lần lượt tại các điểm M, N, P, Q.
Giải sách bài tập Toán 11 Bài 11: Hai đường thẳng song song - Kết nối tri thức
Bài 4.19 trang 60 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Một mặt phẳng cắt bốn cạnh AB, BC, CD, DA lần lượt tại các điểm M, N, P, Q.
a) Chứng minh rằng các đường thẳng MN, PQ, AC đôi một song song hoặc đồng quy.
b) Chứng minh rằng các đường thẳng MQ, NP, BD đôi một song song hoặc đồng quy.
Lời giải:
a)
Ta có (ABC) ∩ (ACD) = AC;
(ABC) ∩ (MNPQ) = MN;
(ACD) ∩ (MNPQ) = PQ.
Khi đó ba mặt phẳng (ABC), (ACD) và (MNPQ) đôi một cắt nhau theo ba giao tuyến AC, MN, PQ. Áp dụng định lí về ba đường giao tuyến cho ba mặt phẳng trên, ta suy ra ba đường thẳng MN, PQ, AC đôi một song song hoặc đồng quy.
b) Ta có (ABD) ∩ (BCD) = BD;
(ABD) ∩ (MNPQ) = MQ;
(BCD) ∩ (MNPQ) = NP.
Khi đó ba mặt phẳng (ABD), (BCD) và (MNPQ) đôi một cắt nhau theo ba giao tuyến MQ, NP, BD. Áp dụng định lí về ba đường giao tuyến cho ba mặt phẳng trên, ta suy ra ba đường thẳng MQ, NP, BD đôi một song song hoặc đồng quy.
Lời giải SBT Toán 11 Bài 11: Hai đường thẳng song song hay khác: