Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là một điểm bất kì thuộc cạnh SC
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là một điểm bất kì thuộc cạnh SC.
Giải sách bài tập Toán 11 Bài 11: Hai đường thẳng song song - Kết nối tri thức
Bài 4.14 trang 59 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là một điểm bất kì thuộc cạnh SC.
a) Xác định các giao tuyến của mặt phẳng (MAB) với các mặt của hình chóp.
b) Xác định các giao tuyến của mặt phẳng (MAD) với các mặt của hình chóp.
Lời giải:
a)
Giao tuyến của mặt phẳng (MAB) với mặt phẳng (ABCD) là AB.
Giao tuyến của mặt phẳng (MAB) với mặt phẳng (SAB) là AB.
Giao tuyến của mặt phẳng (MAB) với mặt phẳng (SBC) là MB.
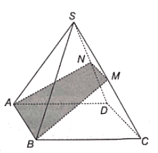
Trong mặt phẳng (SCD), vẽ MN // CD (N ∈ SD).
Mà AB // CD (do ABCD là hình bình hành) nên MN // AB // CD.
Do đó, N thuộc mặt phẳng (MAB) nên giao tuyến của của mặt phẳng (MAB) với mặt phẳng (SCD) là MN và giao tuyến của mặt phẳng (MAB) với mặt phẳng (SAD) là NA.
b)
Giao tuyến của mặt phẳng (MAD) với mặt phẳng (ABCD) là AD.
Giao tuyến của mặt phẳng (MAD) với mặt phẳng (SAD) là AD.
Giao tuyến của mặt phẳng (MAD) với mặt phẳng (SCD) là MD.
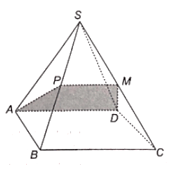
Trong mặt phẳng (SBC), vẽ MP // BC (P ∈ SB).
Mà AD // BC (do ABCD là hình bình hành) nên MP // AD // BC.
Do đó, P thuộc mặt phẳng (MAD) nên giao tuyến của của mặt phẳng (MAD) với mặt phẳng (SBC) là MP và giao tuyến của mặt phẳng (MAD) với mặt phẳng (SAB) là AP.
Lời giải SBT Toán 11 Bài 11: Hai đường thẳng song song hay khác: