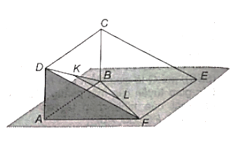
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi K và L lần lượt là giao điểm của hai đường chéo của hai hình bình thành đó. Chứng minh rằng:
Giải sách bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức
Bài 4.23 trang 63 SBT Toán 11 Tập 1: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi K và L lần lượt là giao điểm của hai đường chéo của hai hình bình thành đó. Chứng minh rằng:
a) KL // (ADF);
b) KL // (BCE).
Lời giải:
a) Vì Gọi K và L lần lượt là giao điểm của hai đường chéo của hai hình bình hành ABCD và ABEF nên K và L lần lượt là trung điểm của các đường chéo BD và BF.
Khi đó, KL là đường trung bình của tam giác BDF nên KL // DF, suy ra KL // (ADF).
b) Tương tự câu a, ta có KL là đường trung bình của tam giác ACE nên KL // CE, suy ra KL // (BCE).
Lời giải SBT Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay khác: