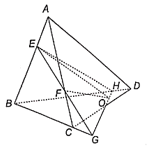
Cho tứ diện ABCD. Gọi E, F là các điểm lần lượt thuộc các cạnh AB, AC
Cho tứ diện ABCD. Gọi E, F là các điểm lần lượt thuộc các cạnh AB, AC sao cho AE = BE và AF = 2CF. Gọi O là một điểm nằm trong tam giác BCD.
Giải sách bài tập Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian - Kết nối tri thức
Bài 4.6 trang 55 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi E, F là các điểm lần lượt thuộc các cạnh AB, AC sao cho AE = BE và AF = 2CF. Gọi O là một điểm nằm trong tam giác BCD.
a) Xác định giao tuyến của hai mặt phẳng (OEF) và (ABD).
b) Xác định giao điểm (nếu có) của đường thẳng AD và mặt phẳng (OEF).
Lời giải:
a) Trong mặt phẳng (ABC), gọi G là giao điểm của EF và BC.
Trong mặt phẳng (BCD), gọi H là giao điểm của OG và BD.
Khi đó H là một điểm chung của hai mặt phẳng (OEF) và (ABD).
Lại có E ∈ (OEF) và E ∈ AB ⊂ (ABD) nên E ∈ (OEF) ∩ (ABD).
Vậy EH là giao tuyến của hai mặt phẳng (OEF) và (ABD).
b) Trong mặt phẳng (ABD), gọi I là giao điểm (nếu có) của EH và AD.
Mà EH ⊂ (OEF). Khi đó I là giao điểm của AD và (OEF).
Lời giải SBT Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian hay khác: