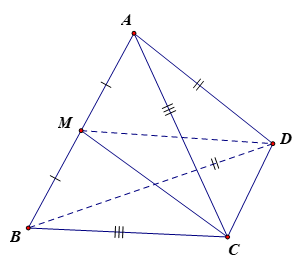
Cho tứ diện ABCD có AC = BC, AD = BD

Cho tứ diện ABCD có AC = BC, AD = BD. Gọi M là trung điểm của AB. Chứng minh rằng (CDM) (ABD).

Giải sách bài tập Toán 11 Bài 25: Hai mặt phẳng vuông góc - Kết nối tri thức

Bài 7.20 trang 34 SBT Toán 11 Tập 2: Cho tứ diện ABCD có AC = BC, AD = BD. Gọi M là trung điểm của AB. Chứng minh rằng (CDM) $⊥$ (ABC) và (CDM) $⊥$ (ABD).

Lời giải:

Xét tam giác ABC có AC = BC nên tam giác ABC cân tại C mà CM là trung tuyến nên CM là đường cao hay CM $⊥$ AB.

Xét tam giác ADB có AD = BD nên tam giác ABD cân tại D mà DM là trung tuyến nên DM là đường cao hay DM $⊥$ AB.

Do đó AB $⊥$ (CDM) mà AB $\subset$ (ABC) nên (CDM) $⊥$ (ABC).

Vì AB $⊥$ (CDM) mà AB $\subset$ (ABD) nên (CDM) $⊥$ (ABD).

Lời giải SBT Toán 11 Bài 25: Hai mặt phẳng vuông góc hay khác:

Xem thêm lời giải Sách bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯