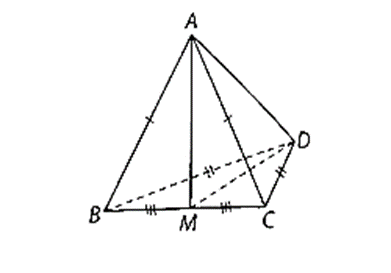
Cho tứ diện ABCD có AB = AC và DB = DC
Cho tứ diện ABCD có AB = AC và DB = DC. Chứng minh rằng AD BC.
Giải sách bài tập Toán 11 Bài 23: Đường thẳng vuông góc với mặt phẳng - Kết nối tri thức
Bài 7.8 trang 28 SBT Toán 11 Tập 2: Cho tứ diện ABCD có AB = AC và DB = DC. Chứng minh rằng AD BC.
Lời giải:
Gọi M là trung điểm của BC.
Xét tam giác ABC có AB = AC và AM là trung tuyến nên AM là đường cao.
Do đó AM BC. (1)
Xét tam giác BCD có DC = DB và DM là trung tuyến nên DM là đường cao.
Do đó DM BC. (2)
Từ (1) và (2) có: BC (ADM). Suy ra BC AD.
Lời giải SBT Toán 11 Bài 23: Đường thẳng vuông góc với mặt phẳng hay khác: