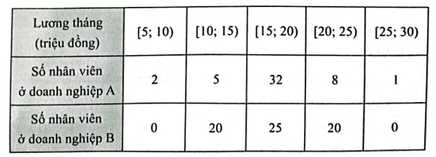
Bảng sau thống kê lương tháng của các nhân viên ở hai doanh nghiệp A và B

---

Bảng sau thống kê lương tháng của các nhân viên ở hai doanh nghiệp A và B:

Giải SBT Toán 12 Chân trời sáng tạo Bài 1: Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm

Bài 4 trang 96 SBT Toán 12 Tập 1: Bảng sau thống kê lương tháng của các nhân viên ở hai doanh nghiệp A và B:

a) Hãy so sánh độ phân tán của mức lương ở hai doanh nghiệp theo khoảng biến thiên.

b) Hãy so sánh độ phân tán của mức lương ở hai doanh nghiệp theo khoảng tứ phân vị.

c) Biết rằng có 1 nhân viên ở doanh nghiệp A có lương tháng là 27 triệu đồng. Lương tháng của nhân viên này có phải là một giá trị ngoại lệ không? Tại sao?

Lời giải:

a) Khoảng biến thiên của mức lương ở doanh nghiệp A là R^A = 30 – 5 = 25 (triệu đồng).

    Khoảng biến thiên của mức lương ở doanh nghiệp B là R^B = 25 – 10 = 15 (triệu đồng).

Nếu so sánh theo khoảng biến thiên thì mức lương ở doanh nghiệp A phân tán hơn mức lương ở doanh nghiệp B.

b) Với mẫu số liệu của doanh nghiệp A, ta có:

Cỡ mẫu là: n = 2 + 5 + 32 + 8 + 1 = 48.

Ta có: : $\frac{n}{4}=\frac{48}{4}=12$.

Tứ phân vị thứ nhất của mẫu số liệu gốc là x₁₂ ∈ [15; 20).

Do đó, Q₁ = 15 + $\frac{12-\left(2+5\right)}{32}\left(20-15\right)$ = $\frac{505}{32}$.

Ta có: $\frac{3n}{4}=\frac{3.48}{4}=36$.

Tứ phân vị thứ ba của mẫu số liệu gốc là x₃₆ ∈ [15; 20).

Do đó, Q₃ = 15 + $\frac{36-\left(2+5\right)}{32}\left(20-15\right)$ = $\frac{625}{32}$.

Vậy khoảng tứ phân vị của mức lương ở doanh nghiệp A là

∆Q_A = Q₃ – Q₁ = $\frac{625}{32}$ − $\frac{505}{32}$ = $\frac{15}{4}$ = 3,75.

Với mẫu số liệu ở doanh nghiệp B, ta có:

Cỡ mẫu là: n = 20 + 25 + 20 = 65.

Ta có: : $\frac{n}{4}=\frac{65}{4}=16,25$.

Tứ phân vị thứ nhất của mẫu số liệu gốc là x₁₇ ∈ [10; 15).

Do đó, Q₁ = 10 + $\frac{16,25-0}{20}\left(15-10\right)$ = $\frac{225}{16}$.

Ta có: $\frac{3n}{4}=\frac{3.65}{4}=48,75$.

Tứ phân vị thứ ba của mẫu số liệu gốc là x₄₉ ∈ [20; 25).

Do đó, Q₃ = 20 + $\frac{48,75-\left(20+25\right)}{20}\left(25-20\right)$ = $\frac{335}{16}$.

Vậy khoảng tứ phân vị của mức lương ở doanh nghiệp B là

∆Q_B = Q₃ – Q₁ = $\frac{335}{16}$ − $\frac{225}{16}$ = $\frac{55}{8}$ = 6,875.

Vậy nếu so sánh theo khoảng tứ phân vị thì mức lương ở doanh nghiệp B phân tán hơn mức lương ở doanh nghiệp A.

c) Với số liệu ghép nhóm của doanh nghiệp A, ta có:

Q₃ + 1,5∆Q = $\frac{625}{32}$ + 1,5.3,75 ≈ 25,16 < 27.

Do đó, lương tháng 27 triệu động của nhân viên là giá trị ngoại lê.

Lời giải SBT Toán 12 Bài 1: Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm hay khác:

• Bài 1 trang 95 SBT Toán 12 Tập 1: Thời gian đọc sách của một số người cao tuổi trong một tuần được ghi lại ở bảng sau:....

• Bài 2 trang 96 SBT Toán 12 Tập 1: Bảng sau cho biết thời gian hoàn thành cự li đi bộ 10 000 m của một số học sinh:....

• Bài 3 trang 96 SBT Toán 12 Tập 1: Một công ty du lịch ghi lại độ tuổi các du khách đặt một tour du lịch mạo hiểm ở bảng sau: ....

• Bài 5 trang 97 SBT Toán 12 Tập 1: Kết quả khảo sát cân nặng của 80 con tôm càng xanh 5 tháng tuổi ở một khu nuôi tôm được biểu diễn ở biểu đồ tần số dưới đây.....