Cho hình hộp ABCD.A'B'C'D' có A(2; 0; 2), B(4; 2; 4), D(2; −2; 2), C' (8; 10; −10)

Cho hình hộp ABCD.A'B'C'D' có A(2; 0; 2), B(4; 2; 4), D(2; −2; 2), C' (8; 10; −10). Tìm tọa độ điểm A'.

Giải SBT Toán 12 Chân trời sáng tạo Bài 2: Toạ độ của vectơ trong không gian

Bài 6 trang 71 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D' có A(2; 0; 2), B(4; 2; 4), D(2; −2; 2), C' (8; 10; −10). Tìm tọa độ điểm A'.

Lời giải:

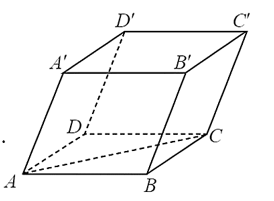
Ta có ABCD là hình bình hành, nên $\overrightarrow{DC}=\overrightarrow{AB}$ = (2; 2; 2).

Gọi C(x; y; z) suy ra $\left\{\begin{array}{l}x-2=2\\ y+2=2\\ z-2=2\end{array}\right.\Rightarrow \left\{\begin{array}{l}x=4\\ y=0\\ z=4\end{array}\right.$ ⇒ C(4; 0; 4).

Ta có: AA'C'C là hình bình hành, suy ra $\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{C{C}^{\text{'}}}$ = (4; 10; −14).

Gọi A'(a; b; c) suy ra $\left\{\begin{array}{l}a-2=4\\ b-0=10\\ c-2=-14\end{array}\right.\Rightarrow \left\{\begin{array}{l}a=6\\ b=10\\ c=-12\end{array}\right.$⇒ A'(6; 10; −12).

Lời giải SBT Toán 12 Bài 2: Toạ độ của vectơ trong không gian hay khác:

• Bài 1 trang 70 SBT Toán 12 Tập 1: Cho điểm M(2; 3; 5) và vectơ $\overrightarrow{a}$ = (2; 0; −7).....

• Bài 2 trang 70 SBT Toán 12 Tập 1: Cho A(4; −3; 1) và vectơ $\overrightarrow{u}$ = (5; 2; −3). Biểu diễn các vectơ sau đây theo các vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$.....

• Bài 3 trang 70 SBT Toán 12 Tập 1: Cho điểm M(9; 3; 6). Gọi M₁, M₂, M₃ lần lượt là hình chiếu của điểm M trên các trục tọa độ Ox, Oy, Oz....

• Bài 4 trang 71 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D' có A(5; 7; −4), B(6; 8; −4), C(6; 7; −3), D'(3; 0; 3). Tìm tọa độ các điểm D và A'....

• Bài 5 trang 71 SBT Toán 12 Tập 1: Cho điểm M(5; −7; −2) và vectơ $\overrightarrow{a}$ = (−3; 0; 1) Hãy biểu diễn mỗi vectơ sau theo hướng các vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$.....

• Bài 7 trang 71 SBT Toán 12 Tập 1: Trên một sân tennis có kích thước như trong Hình 14a), người ta đã thiết lập một hệ tọa độ Oxyz ...