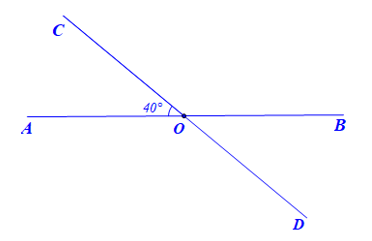
Cho hai đường thẳng AB và CD cắt nhau tại O tạo thành góc AOC = 40 độ

Cho hai đường thẳng AB và CD cắt nhau tại O tạo thành

Giải SBT Toán 7 Chân trời sáng tạo Bài 2: Tia phân giác

Bài 4 trang 79 sách bài tập Toán lớp 7 Tập 1: Cho hai đường thẳng AB và CD cắt nhau tại O tạo thành $\widehat{AOC}=40°.$

a) Tính số đo các góc còn lại.

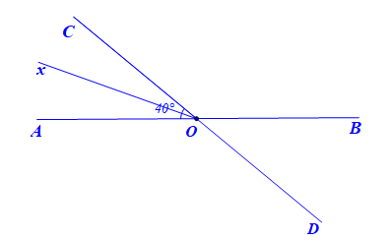
b) Vẽ Ox là tia phân giác của $\widehat{AOC}.$ Hãy tính số đo của $\widehat{xOD}$ và $\widehat{xOB}.$

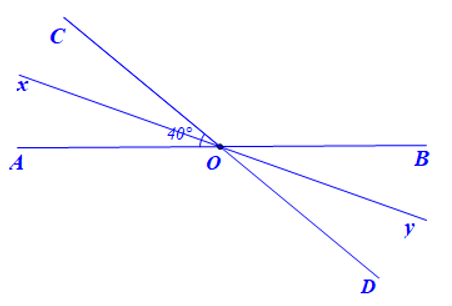
c) Vẽ Oy là tia đối của tia Ox. Chứng tỏ rằng Oy là tia phân giác của $\widehat{BOD}.$

Lời giải:

a)

Ta có:

• $\widehat{AOC}$ và $\widehat{BOD}$ là hai góc đối đỉnh nên:

$\widehat{AOC}=\widehat{BOD}=40°.$

• $\widehat{AOC}$ và $\widehat{BOC}$ là hai góc kề bù nên:

$\widehat{AOC}+\widehat{BOC}=180°.$

Suy ra $\widehat{BOC}=180°-\widehat{AOC}=180°-40°=140°.$

• $\widehat{AOD}$ và $\widehat{BOC}$ là hai góc đối đỉnh nên:

$\widehat{AOD}=\widehat{BOC}=140°.$

Vậy $\widehat{BOD}=40°,$ $\widehat{BOC}=140°$ và $\widehat{AOD}=140°.$

b)

• Vì tia Ox là tia phân giác của $\widehat{AOC}$ nên ta có:

$\widehat{\text{AOx}}=\widehat{xOC}=\frac{1}{2}\widehat{AOC}=\frac{1}{2}.40°=20°.$

• Vì $\widehat{AOx}$ và $\widehat{AOD}$ là hai góc kề nhau nên ta có:

$\widehat{AOx}+\widehat{AOD}=\widehat{xOD}$

Suy ra $\widehat{xOD}=20°+140°=160°.$

• Vì $\widehat{xOC}$ và $\widehat{BOC}$> là hai góc kề nhau nên ta có:

$\widehat{xOC}+\widehat{BOC}=\widehat{xOB}$

Suy ra $\widehat{xOB}=20°+140°=160°.$

Vậy $\widehat{xOD}°=160°,$ $\widehat{xOB}=160°.$

c)

Ta có

• $\widehat{xOA}$ và $\widehat{yOD}$ là hai góc đối đỉnh nên:

$\widehat{xOA}=\widehat{yOD}=20°.$

• $\widehat{xOC}$ và $\widehat{yOB}$ là hai góc đối đỉnh nên:

$\widehat{xOC}=\widehat{yOB}=20°.$

Suy ra $\widehat{yOB}=\widehat{yOD}=20°.$

Vậy tia Oy là tia phân giác của $\widehat{BOD}.$