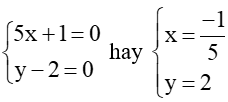Tìm giá trị nhỏ nhất của mỗi biểu thức sau: a) A = 4x^2 ‒ 4x + 23
Tìm giá trị nhỏ nhất của mỗi biểu thức sau:
Giải SBT Toán 8 Bài 3: Hằng đẳng thức đáng nhớ - Cánh diều
Bài 20 trang 15 SBT Toán 8 Tập 1: Tìm giá trị nhỏ nhất của mỗi biểu thức sau:
a) A = 4x2 ‒ 4x + 23;
b) B = 25x2 + y2 + 10x ‒ 4y + 2.
Lời giải:
a) Ta có: A = 4x2 ‒ 4x + 23 = (4x2 ‒ 4x + 1) + 22 = (2x ‒ 1)2 + 22.
Mà (2x ‒ 1)2 ≥ 0 với mọi x
⇒(2x ‒ 1)2 + 22 ≥ 22 với mọi x.
Vậy giá trị nhỏ nhất của A là 22 khi 2x ‒ 1 = 0 hay .
b) Ta có: B = 25x2 + y2 + 10x ‒ 4y + 2
= (25x2 + 10x + 1) + (y2 ‒ 4y + 4) ‒ 3
= (5x + 1)2 + (y ‒ 2)2 ‒ 3.
Mà (5x + 1)2 ≥ 0; (y ‒ 2)2 ≥ 0 với mọi x và y
⇒ (5x + 1)2 + (y ‒ 2)2 ‒ 3 ≥ ‒3 với mọi x và y.
Vậy giá trị nhỏ nhất của B là –3 khi và chỉ khi
Lời giải SBT Toán 8 Bài 3: Hằng đẳng thức đáng nhớ hay khác: