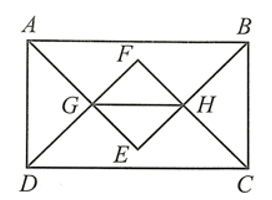
Cho hình chữ nhật ABCD có hai cạnh kề không bằng nhau
Giải SBT Toán 8 Bài 7: Hình vuông - Cánh diều
Bài 32 trang 102 SBT Toán 8 Tập 1: Cho hình chữ nhật ABCD có hai cạnh kề không bằng nhau. Tia phân giác của các góc A và B cắt nhau tại E. Tia phân giác của các góc C và D cắt nhau tại F. Gọi G là giao điểm của AE và DF, H là giao điểm của BE và CF. Chứng minh:
a) GH // CD;
b) Tứ giác GFHE là hình vuông.
Lời giải:
a) Do ABCD là hình chữ nhật nên
Mà AE, BE, CF, DF lần lượt là các tia phân giác của các
Suy ra
Xét ∆ADG có:
Suy ra
Do đó ∆ADG vuông cân tại G
Chứng minh tương tự các tam giác EAB, FCD, HBC đều là tam giác vuông cân.
Xét ∆GAD và ∆HBC có:
, cạnh AD = BC (do ABCD là hình chữ nhật)
Do đó ∆GAD = ∆HBC (g.c.g).
Suy ra GD = HC (hai cạnh tương ứng).
Mà FD = FC, suy ra FG = FH.
∆GFH có: và FG = FH
Do đó, tam giác FGH vuông cân tại F. Suy ra .
Ta có: và nằm ở vị trí đồng vị nên GH // CD.
b) Ta có (hai góc đối đỉnh).
Tứ giác GFHE có nên GFHE là hình chữ nhật.
Hình chữ nhật GFHE có FG = FH nên GFHE là hình vuông.
Lời giải SBT Toán 8 Bài 7: Hình vuông hay khác: