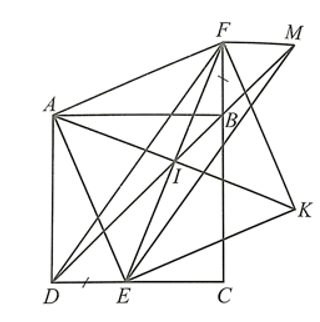
Cho hình vuông ABCD Lấy điểm E thuộc cạnh CD và điểm F

Giải SBT Toán 8 Bài 7: Hình vuông - Cánh diều

Bài 36 trang 103 SBT Toán 8 Tập 1: Cho hình vuông ABCD. Lấy điểm E thuộc cạnh CD và điểm F thuộc tia đối của tia BC sao cho BF = DE.

a) Chứng minh tam giác AEF là tam giác vuông cân.

b) Gọi I là trung điểm của EF. Trên tia đối của tia IA lấy điểm K sao cho IK = IA. Chứng minh tứ giác AEKF là hình vuông.

c*) Chứng minh I thuộc đường thẳng BD.

Lời giải:

Cho hình vuông ABCD Lấy điểm E thuộc cạnh CD và điểm F

a) Do ABCD là hình vuông nên AB = AD, $\hat{A D E} = \hat{A B C} = \hat{B A D} = 90 °$

Mà $\hat{A B C} + \hat{A B F} = 180 °$ nên $\hat{A B F} = 180 ° - \hat{A B C} = 180 ° - 90 ° = 90 °$

Xét ∆ADE và ∆ABF có:

$\hat{A D E} = \hat{A B F} = 90 °$ , AD = AB, DE = BF

Do đó ∆ADE = ∆ABF (c.g.c).

Suy ra AE = AF và $\hat{D A E} = \hat{B A F}$ .

Từ đó ta có $\hat{D A E} + \hat{B A E} = \hat{B A F} + \hat{B A E}$

Hay $\hat{B A D} = \hat{E A F}$ . Do đó $\hat{E A F} = 90 °$ .

Tam giác AEF có $\hat{E A F} = 90 °$ , AE = AF nên tam giác AEF vuông cân tại A.

b) Do IK = IA nên I là trung điểm của AK.

Tứ giác AEKF có hai đường chéo AK, EF cắt nhau tại trung điểm I của mỗi đường nên AEKF là hình bình hành.

Hình bình hành AEKF có $\hat{E A F} = 90 °$ nên AEKF là hình chữ nhật.

Hình chữ nhật AEKF có AE = AF nên AEKF là hình vuông.

c*) Từ điểm F kẻ đường thẳng song song với CD cắt đường thẳng BD tại M.

Do ABCD là hình vuông nên $\hat{C B D} = \frac{\hat{C B A}}{2} = \frac{90 °}{2} = 45 °$ .

Mà $\hat{F B M} = \hat{C B D}$ (hai góc đối đỉnh), suy ra $\hat{F B M} = 45 °$ .

Do MF // CD nên $\hat{B F M} = \hat{B C D} = 90 °$ (cặp góc so le trong).

Tam giác FBM có $\hat{B F M} = 45 °$ và $\hat{F B M} = 45 °$ nên tam giác FBM vuông cân tại F.

Suy ra MF = BF.

Mà BF = DE, suy ra MF = DE.

Tứ giác DEMF có MF = DE và MF // DE nên DEMF là hình bình hành.

Mà I là trung điểm của EF, suy ra I là trung điểm của DM.

Vậy I thuộc đường thẳng DM hay I thuộc đường thẳng BD.

Lời giải SBT Toán 8 Bài 7: Hình vuông hay khác: