Cho hình vuông ABCD có AB = 12 cm Trên cạnh CD lấy điểm E

---

Giải SBT Toán 8 Bài 7: Hình vuông - Cánh diều

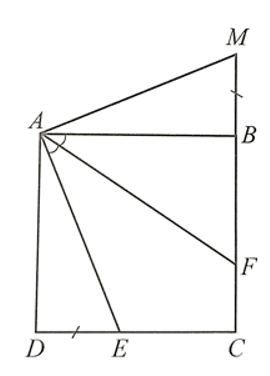
Bài 35 trang 103 SBT Toán 8 Tập 1: Cho hình vuông ABCD có AB = 12 cm. Trên cạnh CD lấy điểm E sao cho DE = 5 cm. Tia phân giác của góc BAE cắt BC tại F. Trên tia đối của tia BC lấy điểm M sao cho BM = DE.

a) Chứng minh AE = AM = FM.

b) Tính độ dài BF.

Lời giải:

a) Do ABCD là hình vuông nên AB = AD, $\widehat{ADC}=\widehat{ABC}=90°$

Ta có: $\widehat{ABM}+\widehat{ABC}=180°$ (2 góc kề bù) nên $\widehat{ABM}=180°-\widehat{ABC}=180°-90°=90°$

Xét ∆ADE và ∆ABM có:

$\widehat{ADE}=\widehat{ABM}=90°$, AD = AB, DE = BM

Do đó ∆ADE = ∆ABM (hai cạnh góc vuông)

Suy ra AE = AM (1) và $\widehat{DAE}=\widehat{BAM}$.

Do AF là tia phân giác của $\widehat{BAE}$ nên $\widehat{EAF}=\widehat{BAF}$.

Suy ra $\widehat{DAE}+\widehat{EAF}=\widehat{BAM}+\widehat{BAF}$ hay $\widehat{DAF}=\widehat{MAF}$.

Mà $\widehat{DAF}=\widehat{MFA}$ (hai góc so le trong do AD // BC), suy ra $\widehat{MFA}=\widehat{MAF}$.

Do đó, tam giác MAF cân tại M nên AM = FM (2)

Từ (1) và (2) suy ra AE = AM = FM.

b) Áp dụng định lý Pythagore cho tam giác ADE vuông tại D, ta có: AE² = AD² + DE²

Suy ra AE² = 12² + 5² = 144 + 25 = 169

Do đó AE = 13 cm.

Mà FM = AE, suy ra FM = 13 cm.

Ta có: FM = BM + BF.

Mà BM = DE = 5 cm  và FM = 13 cm

Suy ra BF = FM – BM = 13 ‒ 5 = 8 cm.

Lời giải SBT Toán 8 Bài 7: Hình vuông hay khác:

• Bài 31 trang 102 SBT Toán 8 Tập 1: Cho hình vuông ABCD có hai đường chéo AC và BD cắt nhau tại O ....

• Bài 32 trang 102 SBT Toán 8 Tập 1: Cho hình chữ nhật ABCD có hai cạnh kề không bằng nhau ....

• Bài 33 trang 102 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Ở phía ngoài hình bình hành, vẽ các hình vuông ABEF ....

• Bài 34 trang 102 SBT Toán 8 Tập 1: Cho tam giác ABC có các đường trung tuyến BD, CE cắt nhau tại G ....

• Bài 36 trang 103 SBT Toán 8 Tập 1: Cho hình vuông ABCD. Lấy điểm E thuộc cạnh CD và điểm F thuộc tia đối ....