Cho hình bình hành ABCD. Ở phía ngoài hình bình hành

Giải SBT Toán 8 Bài 7: Hình vuông - Cánh diều

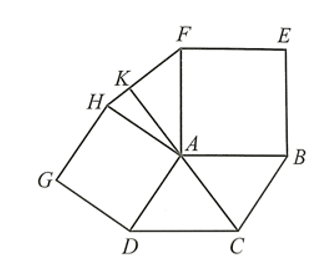
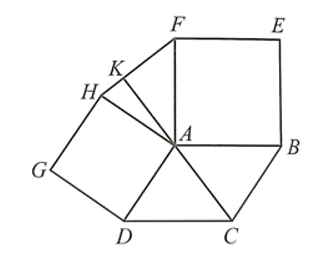
Bài 33 trang 102 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Ở phía ngoài hình bình hành, vẽ các hình vuông ABEF và ADGH (Hình 26).

Chứng minh:

a) DHAF = DADC.

b*) AC ⊥ HF.

Lời giải:

Cho hình bình hành ABCD. Ở phía ngoài hình bình hành

Gọi K là giao điểm của AC và HF.

a) Do ABEF và ADGH đều là hình vuông nên $\hat{B A F} = \hat{D A H} = 90 °$ , AF = AB, AH = AD.

Do ABCD là hình bình hành nên AB = DC

Mà AF = AB nên AF = DC.

Ta có: $\hat{H A F} + \hat{F A B} + \hat{D A B} + \hat{D A H} = 360 °$

Mà $\hat{B A F} = \hat{D A H} = 90 °$ nên $\hat{H A F} + \hat{D A B} = 360 ° - (90 ° + 90 °) = 180 °$ (1)

Hình bình hành ABCD có AB // DC nên $\hat{A D C} + \hat{D A B} = 180 °$ (2)

Từ (1) và (2) suy ra $\hat{H A F} = \hat{A D C}$ .

Xét ∆HAF và ∆ADC có:

AH = AD, $\hat{H A F} = \hat{A D C}$ , AF = DC

Suy ra DHAF = DADC (c.g.c).

b*) Ta có: $\hat{H A K} + \hat{D A H} + \hat{D A C} = \hat{C A K} = 180 °$ và $\hat{D A H} = 90 °$ nên $\hat{H A K} + \hat{D A C} = 90 °$ .

Mà $\hat{A H F} = \hat{D A C}$ (vì DHAF = DADC chứng minh câu a), suy ra $\hat{H A K} + \hat{A H F} = 90 °$ .

Trong tam giác AHK, ta có: $\hat{A K H} + \hat{H A K} + \hat{A H F} = 180 °$ .

Suy ra $\hat{A K H} = 180 ° - (\hat{H A K} + \hat{A H F}) = 180 ° - 90 ° = 90 °$ .

Vậy AK ⊥ HK hay AC ⊥ HF.

Lời giải SBT Toán 8 Bài 7: Hình vuông hay khác: