Hình 4 mô tả một con mèo bị mắc kẹt ở vị trí B trên cành cây

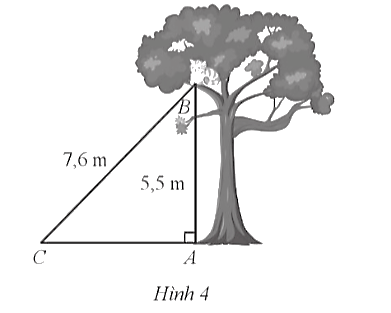
Hình 4 mô tả một con mèo bị mắc kẹt ở vị trí B trên cành cây với độ cao AB = 5,5 m. Để đưa con mèo xuống, người ta cần phải đặt thang dựa vào cành cây đó. Khoảng cách từ chân thang đến điểm chạm vào cành cây là BC = 7,6 m. Góc giữa thang với phương nằm ngang là góc BCA. Tính các tỉ số lượng giác của góc BCA (làm tròn kết quả đến hàng phần trăm).

Giải SBT Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn - Cánh diều

Bài 1 trang 81 SBT Toán 9 Tập 1: Hình 4 mô tả một con mèo bị mắc kẹt ở vị trí B trên cành cây với độ cao AB = 5,5 m. Để đưa con mèo xuống, người ta cần phải đặt thang dựa vào cành cây đó. Khoảng cách từ chân thang đến điểm chạm vào cành cây là BC = 7,6 m. Góc giữa thang với phương nằm ngang là góc BCA. Tính các tỉ số lượng giác của góc BCA (làm tròn kết quả đến hàng phần trăm).

Lời giải:

Trong tam giác ABC vuông tại A, theo định lí Pythagore, ta có:

AB² + AC² = BC².

Suy ra AC² = BC² – AB² = 7,6² – 5,5² = 57,76 – 30,25 = 27,51.

Do đó $AC=\sqrt{27,51}( \text{m}).$

Tam giác ABC vuông tại A nên:

Lời giải SBT Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn hay khác:

• Bài 2 trang 81 SBT Toán 9 Tập 1: Cho tam giác ABC có  $AB=\sqrt{2} \text{cm},$ $BC=\sqrt{5} \text{cm},$ $AC=\sqrt{3} \text{cm}.$ Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.....

• Bài 3 trang 81 SBT Toán 9 Tập 1: Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giá trị mỗi biểu thức sau: a) $\frac{\sin 39°}{\cos 51°};$....

• Bài 4 trang 82 SBT Toán 9 Tập 1: Sử dụng bảng tỉ số lượng giác của các góc nhọn đặc biệt, tính giá trị của mỗi biểu thức sau: a) 2sin30° ‒ 2cos60° + tan45°;....

• Bài 5 trang 82 SBT Toán 9 Tập 1: Tính giá trị của mỗi biểu thức sau: a) A = sin²79° + cos²79°;....

• Bài 6 trang 82 SBT Toán 9 Tập 1: Sử dụng máy tính cầm tay để tính các tỉ số lượng giác của mỗi góc sau (làm tròn kết quả đến hàng phần trăm): a) 47°;....

• Bài 7 trang 82 SBT Toán 9 Tập 1: Một đài quan sát không lưu có độ cao là AB = 95 m. Ở một thời điểm nào đó vào ban ngày, Mặt Trời chiếu tạo bóng dài AC = 200 m trên mặt đất....

• Bài 8 trang 82 SBT Toán 9 Tập 1: Cho Hình 6 có AB = 3 cm, CD = 4 cm. Tính số đo góc AOC (làm tròn kết quả đến hàng đơn vị của độ).....

• Bài 9 trang 82 SBT Toán 9 Tập 1: Từ vị trí B của toà nhà cao 70 m, một tia sáng chiếu xuống một ô tô đang đỗ tại vị trí C. Góc tạo bởi tia sáng và phương nằm ngang ...