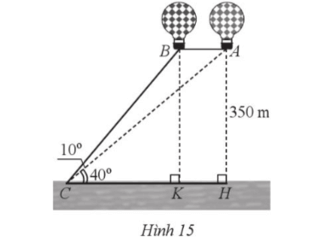
Hai khinh khí cầu được thả lên cùng độ cao là 350 m (ở hai vị trí A và B)

Hai khinh khí cầu được thả lên cùng độ cao là 350 m (ở hai vị trí A và B). Tại vị trí C trên mặt đất, người ta quan sát và đo được (Hình 15). Tính khoảng cách giữa hai khinh khí cầu (làm tròn kết quả đến hàng đơn vị của mét).

Giải SBT Toán 9 Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông - Cánh diều

Bài 16 trang 85 SBT Toán 9 Tập 1: Hai khinh khí cầu được thả lên cùng độ cao là 350 m (ở hai vị trí A và B). Tại vị trí C trên mặt đất, người ta quan sát và đo được $\widehat{ACH}=40°,\widehat{ACB}=10°$ (Hình 15). Tính khoảng cách giữa hai khinh khí cầu (làm tròn kết quả đến hàng đơn vị của mét).

Lời giải:

Vì tam giác ACH vuông tại H nên $CH=AH\cdot \cot \widehat{ACH}=350\cdot \cot 40°.$

Ta có: $\widehat{BCK}=\widehat{BCA}+\widehat{ACH}=10°+40°=50°.$

Vì tam giác BCK vuông tại K nên $CK=BK\cdot \cot \widehat{BCK}=350\cdot \cot 50°.$

Do BK ⊥ CH tại K, AH ⊥ CH tại H suy ra BK // AH.

Mà BK = AH = 350 m

Nên ABKH là hình bình hành.

Suy ra khoảng cách giữa hai khinh khí cầu là:

AB = HK = CH ‒ CK

= 350.cot 40° ‒ 350.cot 50°

= 350.(cot 40° ‒ cot 50°)

≈ 123 m.

Vậy khoảng cách giữa hai khinh khí cầu là khoảng 123 mét.

Lời giải SBT Toán 9 Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông hay khác:

• Bài 10 trang 84 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại C có $AC=\frac{5}{13}AB.$ Tính sin A và tan B....

• Bài 11 trang 84 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A có AB = 21 cm, $\widehat{C}=47°.$ Tính độ dài đường phân giác BD của tam giác ABC ....

• Bài 12 trang 85 SBT Toán 9 Tập 1: Cho tam giác ABC có AB = 6 cm, $\widehat{A}=15°,\widehat{B}=35°.$ Tính độ dài đường cao CH của tam giác ABC....

• Bài 13 trang 85 SBT Toán 9 Tập 1: Tìm x, y trong mỗi hình 14a, 14b, 14c (làm tròn kết quả đến hàng phần mười của centimét).....

• Bài 14 trang 85 SBT Toán 9 Tập 1: Chứng minh diện tích của tam giác đều cạnh a là $\frac{a^2\sqrt{3}}{4}.$....

• Bài 15 trang 85 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A. Chứng minh: $\tan \frac{\widehat{B}}{2}=\frac{AC}{AB+BC}.$....

• Bài 17 trang 85 SBT Toán 9 Tập 1: Bạn Đức đứng trên nóc ngôi nhà ở độ cao 8 m. Vị trí mắt bạn Đức (tại vị trí A) cách nóc nhà 1,5 m. Bạn nhìn thấy vị trí B cao nhất của một toà nhà ....