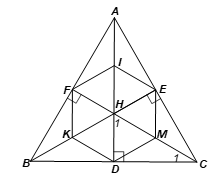
Cho tam giác đều ABC có các đường cao AD, BE, CF cắt nhau tại H
Cho tam giác đều ABC có các đường cao AD, BE, CF cắt nhau tại H. Gọi I, K, M theo thứ tự là trung điểm của HA, HB, HC. Chứng minh lục giác DKFIEM là lục giác đều.
Giải SBT Toán 9 Bài tập cuối chương 9 - Cánh diều
Bài 27 trang 114 SBT Toán 9 Tập 2: Cho tam giác đều ABC có các đường cao AD, BE, CF cắt nhau tại H. Gọi I, K, M theo thứ tự là trung điểm của HA, HB, HC. Chứng minh lục giác DKFIEM là lục giác đều.
Lời giải:
Vì ABC là tam giác đều và CF là đường cao nên CF cũng là đường phân giác của
Suy ra
Tam giác HDC vuông tại D có
⦁ suy ra
⦁ M là trung điểm của HC hay DM là đường trung tuyến ứng với cạnh huyền nên nên MD = MH = MC (cùng bằng một nửa cạnh huyền HC).
Do đó, tam giác DHM là tam giác đều.
Tương tự, ta cũng chứng minh được các tam giác HEM, HEI, HIF, HFK, HKD là các tam giác đều.
Từ đó suy ra lục giác DKFIEM có các góc đều bằng 2.60° = 120° và các cạnh đều bằng nhau, do đó lục giác DKFIEM là lục giác đều.
Lời giải SBT Toán 9 Bài tập cuối chương 9 hay khác: