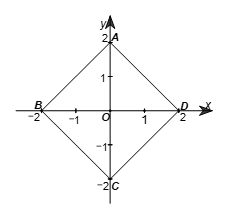
Trên mặt phẳng tọa độ Oxy cho hình vuông ABCD với A(0; 2), B(–2; 0), C(0; –2), D(2; 0)
Trên mặt phẳng tọa độ Oxy cho hình vuông ABCD với A(0; 2), B(–2; 0), C(0; –2), D(2; 0). Phép quay thuận chiều 90° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’. Tính chu vi tứ giác A’B’C’D’.
Giải SBT Toán 9 Bài tập cuối chương 9 - Cánh diều
Bài 30 trang 115 SBT Toán 9 Tập 2: Trên mặt phẳng tọa độ Oxy cho hình vuông ABCD với A(0; 2), B(–2; 0), C(0; –2), D(2; 0). Phép quay thuận chiều 90° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’. Tính chu vi tứ giác A’B’C’D’.
Lời giải:
Do ABCD là hình vuông nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường.
Ta có A(0; 2), B(–2; 0), C(0; –2), D(2; 0) nên B, D cùng nằm trên Ox và A, C cùng nằm trên Oy.
Ta cũng suy ra được OA = OB = OC = OD hay O là tâm của hình vuông ABCD.
Xét ∆OAB vuông tại O, theo định lí Pythagore, ta có:
AB2 = OA2 + OB2 = 22 + 22 = 8.
Suy ra Như vậy, hình vuông ABCD có cạnh bằng
Ta có phép quay thuận chiều 90° tâm O giữ nguyên hình vuông ABCD do đó chu vi tứ giác A’B’C’D’ bằng chu vi hình vuông ABCD và bằng (đơn vị chiều dài).
Lời giải SBT Toán 9 Bài tập cuối chương 9 hay khác: