Cho lục giác đều ABCDEF với tâm O thoả mãn phép quay thuận chiều
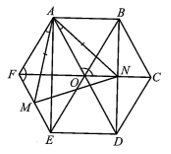
Cho lục giác đều ABCDEF với tâm O thoả mãn phép quay thuận chiều 60° tâm O biến các điểm A, B, C, D, E, F lần lượt thành các điểm B, C, D, E, F, A. Các điểm M, N lần lượt là trung điểm của EF, BD.
Giải SBT Toán 9 Bài tập cuối chương 9 - Cánh diều
Bài 29 trang 114 SBT Toán 9 Tập 2: Cho lục giác đều ABCDEF với tâm O thoả mãn phép quay thuận chiều 60° tâm O biến các điểm A, B, C, D, E, F lần lượt thành các điểm B, C, D, E, F, A. Các điểm M, N lần lượt là trung điểm của EF, BD.
a) Tìm α (0 < α < 180), biết phép quay ngược chiều α° tâm O biến các điểm D, C lần lượt thành các điểm B, A.
b) Chứng minh phép quay thuận chiều 60° tâm A biến các điểm O, N lần lượt thành các điểm F, M.
Lời giải:
a) Do ABCDEF là lục giác đều có tâm O nên OA= OB = OC = OD = OE = OF.
Do phép quay thuận chiều 60° tâm O biến các điểm A, B, C lần lượt thành các điểm B, C, D nên
Do đó
Như vậy, phép quay ngược chiều 120° tâm O biến các điểm D, C lần lượt thành các điểm B, A.
b) Xét lục giác ABCDEF có tổng số đo các góc bằng tổng số đo hai tứ giác ABCD và ADEF, và bằng 2.360° = 720°.
Do ABCDEF là lục giác đều nên các góc của hình lục giác bằng nhau, và bằng
⦁ Xét ∆OAF có OA = OF và nên ∆OAF là tam giác đều, suy ra AF = AO và
Như vậy, phép quay thuận chiều 60° tâm A biến điểm O thành điểm F.
⦁ Xét ∆OBC có OB = OC và nên ∆OBC là tam giác đều, do đó OB = OC = BC.
Chứng minh tương tự, ta sẽ có OB = BC = CD = OD nên tứ giác OBCD là hình thoi, do đó hai đường chéo OC và BD vuông góc với nhau tại trung điểm của mỗi đường.
Theo bài, N là trung điểm của BC nên N là trung điểm của OC, do đó OC = 2ON.
Ta có: M là trung điểm của EF nên EF = 2FM, mà EF = BC = OC nên OC = 2FM.
Suy ra FM = ON.
Xét ∆AFM và ∆AON có:
FA = AO, FM = ON
Do đó ∆AFM = ∆AON (c.g.c).
Suy ra AM = AN và
Do đó,
Có AM = AN và nên phép quay thuận chiều 60° tâm A biến điểm N thành điểm M.
Lời giải SBT Toán 9 Bài tập cuối chương 9 hay khác: