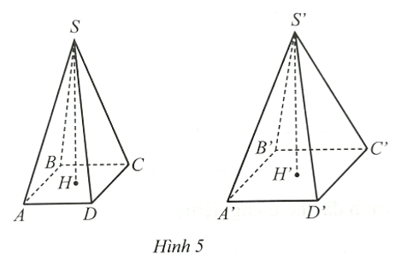
Ở Hình 5, cho hai hình chóp tứ giác đều S.ABCD và S.A’B’C’D’ có cùng chiều cao

---

Ở Hình 5, cho hai hình chóp tứ giác đều có cùng chiều cao . Thể tích của hình chóp nhỏ hơn thể tích của hình chóp là 240 cmTính độ dài cạnh đáy của mỗi hình chóp, biết rằng

Giải SBT Toán 9 Bài tập cuối chương 1 - Cánh diều

Bài 36 trang 23 SBT Toán 9 Tập 1: Ở Hình 5, cho hai hình chóp tứ giác đều S.ABCD và S.A’B’C’D’ có cùng chiều cao SH = S’H’ = 30 cm. Thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S.A’B’C’D’ là 240 cm³. Tính độ dài cạnh đáy của mỗi hình chóp, biết rằng A’B’ ‒ AB = 2 cm.

Lời giải:

Đặt AB = x (cm) và A’B = y (cm) với x > 0 và y > 0.

Theo bài, A’B’ ‒ AB = 2 cm nên ta có: y – x = 2.  (1)

Diện tích đáy của hình chóp tứ giác đều S.ABCD là:

S_ABCD = AB² = x² (cm²).

Thể tích của hình chóp tứ giác đều S.ABCD là:

$\frac{1}{3}\cdot SH\cdot S_{ABCD}=\frac{1}{3}\cdot 30\cdot x^2=10x^2$ (cm³).

Diện tích đáy của hình chóp tứ giác đều S.A’B’C’D’ là:

S_{A’B’C’D’} = A’B’² = y² (cm²).

Thể tích của hình chóp tứ giác đều S.A’B’C’D’ là:

$\frac{1}{3}\cdot S^{\text{'}}{H}^{\text{'}}\cdot S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}=\frac{1}{3}\cdot 30\cdot y^2=10y^2$ (cm³).

Theo bài, thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S.A’B’C’D’ là 240 cm³ nên ta có phương trình:

10y² – 10x² = 240

y² – x² = 24

(y – x)(y + x) = 24

2.(y + x) = 24         (do y – x = 2)

y + x = 12. (2)

Từ (1) và (2) ta có hệ phương trình: $\left\{\begin{array}{l}y-x=2\left(1\right)\\ y+x=12\left(2\right)\end{array}\right.$

Cộng từng vế hai phương trình (1) và (20, ta nhận được phương trình:

2y = 14, suy ra y = 7.

Thay y = 7 vào phương trình (1), ta có: 7 – x = 2, suy ra x = 7 – 2 = 5.

Ta thấy x = 5 và y = 7 thỏa mãn điều kiện.

Vậy độ dài cạnh đáy của hình chóp S.ABCD và S’.A’B’C’D’ lần lượt là 5 cm và 7 cm.

Lời giải SBT Toán 9 Bài tập cuối chương 1 hay khác:

• Bài 26 trang 21 SBT Toán 9 Tập 1: Tổng các nghiệm của phương trình (x ‒ 3)(2x + 6) = 0 là....

• Bài 27 trang 21 SBT Toán 9 Tập 1: Trong các cặp số (‒1; 0), (2; ‒2), (6; ‒1), (4; ‒3), $\left(0;\frac{-3}{5}\right),$ có bao nhiêu cặp số là nghiệm của phương trình 3x + 5y = ‒3?....

• Bài 28 trang 21 SBT Toán 9 Tập 1: Giải các phương trình sau: a) $\frac{x+1}{x-1}-\frac{x-1}{x+1}=\frac{16}{x^2-1};$...

• Bài 29 trang 22 SBT Toán 9 Tập 1: Giải các hệ phương trình sau bằng phương pháp thế: a) $\left\{\begin{array}{l}x-3y=-2\\ 7x+2y=9;\end{array}\right.$ ....

• Bài 30 trang 22 SBT Toán 9 Tập 1: Giải các hệ phương trình sau bằng phương pháp cộng đại số: a) $\left\{\begin{array}{l}0,7x+0,5y=1,2\\ -x+2y=1;\end{array}\right.$....

• Bài 31 trang 22 SBT Toán 9 Tập 1: Hai khu công nghiệp A và B có tổng cộng 2 200 công nhân. Sau khi chuyển 100 công nhân ở khu A sang khu B ....

• Bài 32 trang 22 SBT Toán 9 Tập 1: Một công ty du lịch tiến hành giảm giá cho gói du lịch loại A trong các dịp lễ:....

• Bài 33 trang 22 SBT Toán 9 Tập 1: Một tam giác có chiều cao bằng $\frac{3}{4}$ cạnh đáy. Nếu tăng chiều cao thêm 3 dm và giảm cạnh đáy đi 3 dm thì diện tích của tam giác tăng thêm 6 dm²....

• Bài 34 trang 22 SBT Toán 9 Tập 1: Hai vòi nước cùng chảy vào một bể không chứa nước thì bể đó đầy nước sau 4 giờ 48 phút. ....

• Bài 35 trang 23 SBT Toán 9 Tập 1: Hai xe máy khởi hành cùng một lúc. Xe máy thứ nhất đi từ địa điểm A đến địa điểm B và xe máy thứ hai đi từ địa điểm B đến địa điểm A ....