Cho đường tròn (O; R) và ba điểm A, B, C nằm trên đường tròn với AB nhỏ hơn AC

---

Cho đường tròn (O; R) và ba điểm A, B, C nằm trên đường tròn với AB

Giải SBT Toán 9 Bài tập cuối chương 5 - Cánh diều

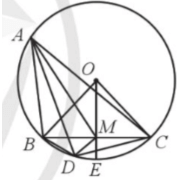
Bài 54 trang 124 SBT Toán 9 Tập 1: Cho đường tròn (O; R) và ba điểm A, B, C nằm trên đường tròn với AB < AC. Gọi M là trung điểm của đoạn thẳng BC. Trên cung BC không chứa điểm A, lấy điểm D sao cho $\widehat{BAD}=\widehat{CAM}.$

a) Chứng minh $\widehat{ADB}=\widehat{CDM}.$

b) Gọi E là giao điểm của tia OM và cung BC. Tính diện tích hình quạt tròn giới hạn bởi các bán kính OE, OC và cung nhỏ CE theo R, biết $BC=R\sqrt{2}.$

Lời giải:

a) Ta có $\widehat{BAD}=\widehat{CAM}$ nên $\widehat{BAD}+\widehat{DAM}=\widehat{CAM}+\widehat{DAM}$ hay $\widehat{BAM}=\widehat{DAC}.$

Xét đường tròn (O) có $\widehat{ABM}=\widehat{ADC}$ (hai góc nội tiếp cùng chắn cung AC)

Xét ∆ABM và ∆ADC có: $\widehat{BAM}=\widehat{DAC}$ và $\widehat{ABM}=\widehat{ADC}.$

Do đó ∆ ABM ᔕ ∆ADC (g.g).

Suy ra $\frac{AB}{AD}=\frac{BM}{DC}$ (tỉ số các cạnh tương ứng)

Mà BM = CM (do M là trung điểm của BC)

Nên $\frac{AB}{AD}=\frac{BM}{DC}=\frac{CM}{CD}$ hay $\frac{AB}{CM}=\frac{AD}{CD}.$

Xét ∆ABD và ∆CMD có:

$\frac{AB}{CM}=\frac{AD}{CD}$và $\widehat{BAD}=\widehat{MCD}$ (hai góc nội tiếp cùng chắn cung BD của đường tròn (O))

Do đó ∆ABD ᔕ ∆CMD (g.g).

Suy ra $\widehat{ADB}=\widehat{CDM}$ (hai góc tương ứng).

b) Do M là trung điểm của BC nên $MC=\frac{BC}{2}=\frac{R\sqrt{2}}{2}.$

Xét ∆OBC cân tại O (do OB = OC) nên đường trung tuyến OM đồng thời là đường cao của tam giác, do đó $\widehat{OMC}=90°.$

Xét ∆OCM vuông tại M, theo định lí Pythagore, ta có: OC² = OM² + MC²

Suy ra $OM=\sqrt{O{C}^2-M{C}^2}=\sqrt{R^2-{\left(\frac{R\sqrt{2}}{2}\right)}^2}=\sqrt{\frac{R^2}{2}}=\frac{R\sqrt{2}}{2}.$

Do đó OM = MC.

Vì vậy, tam giác OCM vuông cân tại M. Suy ra $\widehat{COE}=45°$ hay số đo của cung nhỏ CE bằng 45°.

Diện tích hình quạt tròn giới hạn bởi các bán kính OE, OC và cung nhỏ CE là:

$S=\frac{\pi R^2\cdot 45}{360}=\frac{\pi R^2}{8}$ (đơn vị diện tích).

Lời giải SBT Toán 9 Bài tập cuối chương 5 hay khác:

• Bài 47 trang 123 SBT Toán 9 Tập 1: Trên mặt phẳng toạ độ Oxy, cho điểm A(1; 1). Khi đó, đường tròn (A; 1) ....

• Bài 48 trang 123 SBT Toán 9 Tập 1: Cho các điểm A, B, C, D thuộc đường tròn tâm O đường kính AC = 2 cm với $\widehat{CBD}=55°$ (Hình 51). ....

• Bài 49 trang 123 SBT Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm M, N với OO’ = 24 cm và MN = 10 cm (Hình 52). Khi đó, R bằng: ....

• Bài 50 trang 123 SBT Toán 9 Tập 1: Trong 20 giây, bánh xe của một chiếc xe máy quay được 80 vòng. Độ dài bán kính của bánh xe đó là 25 cm. Khi đó, quãng đường xe máy đi được trong 3 phút là: ....

• Bài 51 trang 123 SBT Toán 9 Tập 1: Diện tích hình vành khuyên tạo bởi hai đường tròn (O; 12 cm) và (O; 7 cm) là: ....

• Bài 52 trang 123 SBT Toán 9 Tập 1: Cho đường tròn tâm O đường kính AB và điểm M di chuyển trên đường tròn (M khác A và B). Vẽ đường tròn (M) tiếp xúc với AB tại H ....

• Bài 53 trang 124 SBT Toán 9 Tập 1: Cho ba đường tròn (A; 10 cm), (B; 15 cm), (C; 15 cm) tiếp xúc ngoài với nhau đôi một. Đường tròn (A) tiếp xúc với (B) và (C) lần lượt tại C’ và B’ ....

• Bài 55 trang 124 SBT Toán 9 Tập 1: Cho nửa đường tròn tâm O đường kính A B. Gọi C, D lần lượt là điểm chính giữa của cung AB, AC.a) Chứng minh $\widehat{BAC}=\widehat{COD}=\widehat{ABC}=\widehat{ACO}.$ ....

• Bài 56 trang 124 SBT Toán 9 Tập 1: Thành phố Hồ Chí Minh có vĩ độ là 10°10’ Bắc. Tìm độ dài cung kinh tuyến từ Thành phố Hồ Chí Minh đến Xích Đạo (làm tròn kết quả đến hàng trăm của kilômét), ....

• Bài 57 trang 124 SBT Toán 9 Tập 1: Cho hình thang vuông ABCD $\left(\widehat{A}=\widehat{B}=90°\right)$ với $\widehat{C}=30°,$ BC = CD = a. Vẽ một phần đường tròn (C; CD) (Hình 54). Tính diện tích của phần tô màu xám theo a ....

• Bài 58 trang 125 SBT Toán 9 Tập 1: Cho hình vành khuyên giới hạn bởi hai đường tròn (O; R), (O; r) với R + r = 1,2 dm, R > r và diện tích hình vành khuyên đó ....

• Bài 59 trang 125 SBT Toán 9 Tập 1: Tam giác Reuleaux là hình tạo nên từ phần giao nhau của ba đường tròn cùng bán kính, tâm của mỗi đường tròn chính là giao điểm của hai đường tròn còn lại ....

• Bài 60 trang 125 SBT Toán 9 Tập 1: Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn sao cho độ dài cung nhỏ AB ....