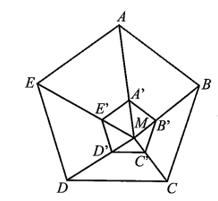
Cho ngũ giác đều ABCDE và một điểm M nằm trong ngũ giác. Gọi A’, B’, C’, D’, E’ lần lượt là các điểm
Cho ngũ giác đều ABCDE và một điểm M nằm trong ngũ giác. Gọi A’, B’, C’, D’, E’ lần lượt là các điểm nằm trên các đoạn thẳng MA, MB, MC, MD, ME sao cho Chứng minh ngũ giác A’B’C’D’E’ là ngũ giác đều.
Giải SBT Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn - Cánh diều
Bài 6 trang 107 SBT Toán 9 Tập 2: Cho ngũ giác đều ABCDE và một điểm M nằm trong ngũ giác. Gọi A’, B’, C’, D’, E’ lần lượt là các điểm nằm trên các đoạn thẳng MA, MB, MC, MD, ME sao cho Chứng minh ngũ giác A’B’C’D’E’ là ngũ giác đều.
Lời giải:
Từ suy ra:
Do đó: A’B’ // AB, B’C’ // BC, C’D’ // CD, D’E’ // DE, E’A’ // EA (định lí Thalès đảo).
Do A’B’ // AB nên (đồng vị);
Do E’A’ // EA nên (đồng vị).
Suy ra
Hay
Chứng minh tương tự, ta được các góc A’, B’, C’, D’, E’ của ngũ giác A’B’C’D’E’ tương ứng bằng các góc A, B, C, D, E của ngũ giác đều ABCDE.
Mà ABCDE là ngũ giác đều nên góc A, B, C, D, E của ngũ giác bằng nhau.
Do đó các góc của ngũ giác A’B’C’D’E’ bằng nhau. (2)
Mặt khác, từ (1) ta cũng chứng minh được:
Mà ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA.
Do đó: A’B’ = B’C’ = C’D’ = D’E’ = E’A’. (3)
Từ (2) và (3) suy ra ngũ giác A’B’C’D’E’ là ngũ giác đều.
Lời giải SBT Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn hay khác:
Bài 1 trang 106 SBT Toán 9 Tập 2: Quan sát Hình 6 và kể tên các đa giác có trong hình đó ....
Bài 5 trang 107 SBT Toán 9 Tập 2: Cho ngũ giác ABCDE. Chứng minh ....