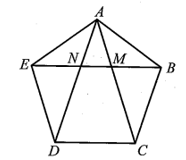
Cho ngũ giác đều ABCDE, đoạn BE cắt các đoạn AC và AD lần lượt tại M và N

Cho ngũ giác đều ABCDE, đoạn BE cắt các đoạn AC và AD lần lượt tại M và N. Chứng minh rằng:

Giải SBT Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn - Cánh diều

Bài 7 trang 107 SBT Toán 9 Tập 2: Cho ngũ giác đều ABCDE, đoạn BE cắt các đoạn AC và AD lần lượt tại M và N. Chứng minh rằng:

a) Các tam giác AEN và CMB là các tam giác cân;

b) AN là phân giác của góc EAM;

c) AB.BC = BM.AC.

Lời giải:

Cho ngũ giác đều ABCDE, đoạn BE cắt các đoạn AC và AD lần lượt tại M và N

a) Ngũ giác ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA và $\hat{A B C} = \hat{B C D} = \hat{C D E} = \hat{D E A} = \hat{E A B} .$

Ta cũng có tổng 5 góc của ngũ giác đều ABCDE bằng tổng các góc của ba tam giác ABC, ACD, ADE, tức là bằng 3.180° = 540°.

Do đó: $\hat{A B C} = \hat{B C D} = \hat{C D E} = \hat{D E A} = \hat{E A B} = \frac{540 °}{5} = 108 ° .$

Xét ∆AEB cân tại A (do AB = AE) ta có:

$\hat{A B E} = \hat{A E B} = \frac{180 ° - \hat{E A B}}{2} = \frac{180 ° - 108 °}{2} = 36 ° .$

Hay $\hat{A B M} = \hat{A E N} = 36 ° .$

Tương tự, đối với ∆EAD cân tại E ta có: $\hat{E A D} = \hat{E D A} = 36 °$ hay $\hat{E A N} = 36 ° .$

Do đó ta có $\hat{E A N} = \hat{N E A} = 36 ° .$ Suy ra ∆AEN cân tại N.

Tương tự, ta chứng minh được ∆MAB cân tại M (do $\hat{M A B} = \hat{M B A} = 36 °)$

Suy ra $\hat{A M B} = 180 ° - 2 \hat{M A B} = 180 ° - 2 \cdot 36 ° = 108 ° .$

Mặt khác: $\hat{C M B} = 180 ° - \hat{A M B} = 180 ° - 108 ° = 72 °;$

$\hat{M B C} = \hat{A B C} - \hat{A B M} = 108 ° - 36 ° = 72 ° .$

Suy ra tam giác CMB cân tại C.

b) Ta có: $\hat{E A B} = \hat{E A N} + \hat{N A M} + \hat{M A B}$

Suy ra $\hat{N A M} = \hat{E A B} - \hat{E A N} - \hat{M A B} = 108 ° - 36 ° - 36 ° = 36 ° .$

Do đó $\hat{E A N} = \hat{N A M} = 36 ° .$

Vì vậy AN là phân giác của góc EAM.

c) Xét ∆MAB và ∆BAC có:

$\hat{A M B} = \hat{A B C} = 108 °$ và $\hat{B A C}$ là góc chung

Do đó ∆MAB ᔕ ∆BAC (g.g), suy ra $\frac{A B}{A C} = \frac{B M}{C B}$ hay AB.BC = BM.AC.

Lời giải SBT Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn hay khác: