Người ta chia đường tròn (O; R) thành 6 cung bằng nhau như sau: Trên đường tròn (O; R), lấy điểm A tuỳ ý
Người ta chia đường tròn (O; R) thành 6 cung bằng nhau như sau:
Giải SBT Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn - Cánh diều
Bài 9 trang 107, 108 SBT Toán 9 Tập 2: Người ta chia đường tròn (O; R) thành 6 cung bằng nhau như sau:
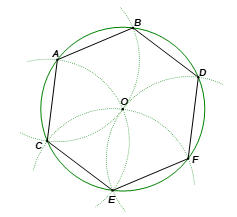
– Trên đường tròn (O; R), lấy điểm A tuỳ ý;
– Vẽ một phần đường tròn (A; R) cắt (O; R) tại B và C;
– Vẽ một phần đường tròn (C; R) cắt (O; R) tại E (khác A);
– Vẽ một phần đường tròn (E; R) cắt (O; R) tại F (khác C);
– Vẽ một phần đường tròn (F; R) cắt (O; R) tại D (khác E).
Nối A với B, B với D, D với F, F với E, E với C, C với A, ta được lục giác ABDFEC.
Chứng minh:
a) Lục giác ABDFEC là lục giác đều;
b) AF, BE, CD là các đường kính của đường tròn (O; R);
c) Các tứ giác ACEF, ABDC, BECA đều là hình thang cân.
Lời giải:
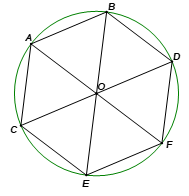
a) Nối OA, OB, OC, OD, OE, OF.
⦁ Từ giả thiết ta có sáu cung AB, AC, CE, EF, FD, DB bằng nhau nên
Xét ∆AOB và ∆BOD có:
OA = OB; OB = OD.
Do đó ∆AOB = ∆BOD (c.g.c), suy ra AB = BD (hai cạnh tương ứng).
Mặt khác, ta có AB = AC = CE = EF = FD = R.
Nên AB = AC = CE = EF = FD = DB. (1)
⦁ Ta có
Suy ra do đó
Xét ∆AOB có OA = OB và nên ∆AOB là tam giác đều.
Do đó
Chứng minh tương tự, ta cũng có ∆OAC đều nên
Khi đó,
Tương tự, ta chứng minh được:
Từ (1) và (2) ta có ABDFEC là lục giác đều.
b) Do ABDFEC là lục giác đều nên ba đường chéo AF, BE, CD cắt nhau tại O.
Do đó AF, BE, CD là các đường kính của đường tròm (O; R).
c) Chứng minh tương tự ở câu a, ta chứng minh được ∆AOC, ∆OCE là các tam giác đều. Suy ra
Mà hai góc này ở vị trí so le trong nên AO // CE hay AF // CE.
Tứ giác ACEF có AF // CE nên là hình thang.
Lại có nên ACEF là hình thang cân.
Chứng minh tương tự, ta cũng có các tứ giác ABDC, BECA đều là hình thang cân.
Lời giải SBT Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn hay khác:
Bài 1 trang 106 SBT Toán 9 Tập 2: Quan sát Hình 6 và kể tên các đa giác có trong hình đó ....
Bài 5 trang 107 SBT Toán 9 Tập 2: Cho ngũ giác ABCDE. Chứng minh ....
Bài 6 trang 107 SBT Toán 9 Tập 2: Cho ngũ giác đều ABCDE và một điểm M nằm trong ngũ giác ....