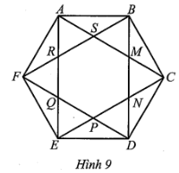
Ở Hình 9 biết ABCDEF là lục giác đều, chứng minh rằng lục giác MNPQRS cũng là lục giác đều
Ở Hình 9 biết ABCDEF là lục giác đều, chứng minh rằng lục giác MNPQRS cũng là lục giác đều.
Giải SBT Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn - Cánh diều
Bài 8 trang 107 SBT Toán 9 Tập 2: Ở Hình 9 biết ABCDEF là lục giác đều, chứng minh rằng lục giác MNPQRS cũng là lục giác đều.
Lời giải:
Lục giác ABCDEF là lục giác đều nên AB = BC = CD = DE = EF = FA và
Ta cũng có tổng 6 góc của lục giác đều ABCDEF bằng tổng các góc của hai tứ giác ABCD và AFED, tức là bằng 2.360° = 720°.
Do đó:
Xét ∆AFB cân tại A (do AB = AF) ta có:
Hay
Tương tự, đối với ∆ABC cân tại B ta có: hay
Do đó ta có Nên ∆ABS cân tại S.
Suy ra
Khi đó, (đối đỉnh).
Chứng minh tương tự, ta được:
Ta có: (kề bù)
Suy ra
Ta cũng có:
Do đó ∆BSM là tam giác cân, lại có nên ∆BSM là tam giác đều.
Suy ra SB = SM = BM.
Chứng minh tương tự ta có ∆SAR là tam giác đều nên SA = SR = AR.
Do ∆ABS cân tại S nên SA = SB.
Khi đó, RS = SM.
Chứng minh tương tự, ta được:
RS = SM = MN = NP = PQ = QR. (2)
Từ (1) và (2) suy ra lục giác MNPQRS là lục giác đều.
Lời giải SBT Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn hay khác:
Bài 1 trang 106 SBT Toán 9 Tập 2: Quan sát Hình 6 và kể tên các đa giác có trong hình đó ....
Bài 5 trang 107 SBT Toán 9 Tập 2: Cho ngũ giác ABCDE. Chứng minh ....
Bài 6 trang 107 SBT Toán 9 Tập 2: Cho ngũ giác đều ABCDE và một điểm M nằm trong ngũ giác ....