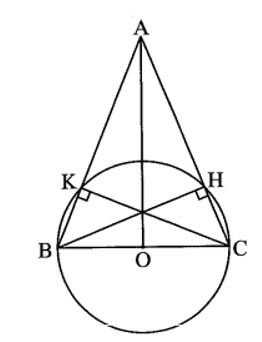
Cho tam giác ABC có AB = AC = 13 cm, BC = 10 cm và có BH, CK là hai đường cao

Cho tam giác ABC có AB = AC = 13 cm, BC = 10 cm và có BH, CK là hai đường cao.

Giải sách bài tập Toán 9 Bài 1: Đường tròn - Chân trời sáng tạo

Bài 2 trang 84 sách bài tập Toán 9 Tập 1: Cho tam giác ABC có AB = AC = 13 cm, BC = 10 cm và có BH, CK là hai đường cao.

Chứng minh:

a) Bốn điểm B, C, H, K cùng nằm trên đường tròn (O; R).

b) Điểm A nằm ngoài đường tròn (O; R).

Lời giải:

Cho tam giác ABC có AB = AC = 13 cm, BC = 10 cm và có BH, CK là hai đường cao

a) Gọi O là trung điểm của BC. Khi đó, $O B = O C = \frac{1}{2} B C .$

Do BH và CK là đường cao tam giác ABC nên BH ⊥ AC tại H; CK ⊥ AB tại K

Suy ra tam giác BHC vuông tại H; tam giác BKC vuông tại K

Xét tam giác BKC vuông tại H có KO là đường trung tuyến ứng với cạnh huyền BC nên $K O = \frac{1}{2} B C .$

Chứng minh tương tự đối với ∆BKC vuông tại K, ta có $H O = \frac{1}{2} B C .$

Suy ra $K O = O H = O B = O C = \frac{1}{2} B C = \frac{1}{2} \cdot 10 = 5 (cm) .$

Tứ giác BKHC có: OB = OK = OH = OC = 5 cm nên bốn điểm B, C, H, K cùng nằm trên đường tròn (O; R) với R = 5 cm.

b) Xét ∆ABC cân tại A (do AB = AC) có AO là đường trung tuyến nên đồng thời là đường cao, suy ra ∆ABO vuông tại O.

Áp dụng định lí Pythagore cho tam giác AOB vuông tại O, ta có:

$O A = \sqrt{B A^{2} - O B^{2}} = \sqrt{13^{2} - 5^{2}} = \sqrt{144} = 12 (cm) .$

Vì 12 > 5 nên OA > R, suy ra điểm A nằm ngoài đường tròn (O; R).

Lời giải SBT Toán 9 Bài 1: Đường tròn hay khác: