Cho đường tròn (O; 8 cm) và hai điểm A, B nằm trên đường tròn thoả mãn AB = 6 cm
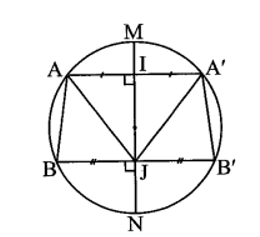
Cho đường tròn (O; 8 cm) và hai điểm A, B nằm trên đường tròn thoả mãn AB = 6 cm. Vẽ đường kính MN sao cho hai đoạn thẳng MN và AB không có điểm chung. Gọi A’, B’ lần lượt là hai điểm đối xứng với A, B qua MN. Chứng minh:
Giải sách bài tập Toán 9 Bài 1: Đường tròn - Chân trời sáng tạo
Bài 4 trang 85 sách bài tập Toán 9 Tập 1: Cho đường tròn (O; 8 cm) và hai điểm A, B nằm trên đường tròn thoả mãn AB = 6 cm. Vẽ đường kính MN sao cho hai đoạn thẳng MN và AB không có điểm chung. Gọi A’, B’ lần lượt là hai điểm đối xứng với A, B qua MN. Chứng minh:
a) ABB’A’ là hình thang cân.
b) Bốn điểm A, B, B’, A’ cùng nằm trên đường tròn (O; 8 cm).
Lời giải:
a) Gọi I, J lần lượt là giao điểm của MN với AA’, BB’.
Do A’, B’ lần lượt là hai điểm đối xứng với A, B qua MN nên AA’ ⊥ MN tại I, IA = IA’ và BB’ ⊥ MN tại J, JB = JB’.
Xét ∆AIJ và ∆A’IJ, có:
IA = IA’, cạnh IJ chung
Do đó ∆AIJ = ∆A’IJ (hai cạnh góc vuông)
Suy ra AJ = A’J và (các cặp cạnh và góc tương ứng).
Ta có: và nên
Xét ∆ABJ và ∆A’B’J, có:
JB = JB’, AJ = A’J
Do đó ∆ABJ = ∆A’B’J (c.g.c), suy ra
Ta có AA’ // BB’ (cùng vuông góc với MN) nên ABB’A’ là hình thang, lại có nên ABB’A’ là hình thang cân.
b) Ta có MN là trục đối xứng của đường tròn (O; 8 cm), A, B đã thuộc đường tròn (O; 8 cm) suy ra A’, B’ là hai điểm đối xứng với A, B qua MN nên cũng thuộc đường tròn (O; 8 cm), suy ra bốn điểm A, B, B’, A’ cùng nằm trên đường tròn (O; 8 cm).
Lời giải SBT Toán 9 Bài 1: Đường tròn hay khác: