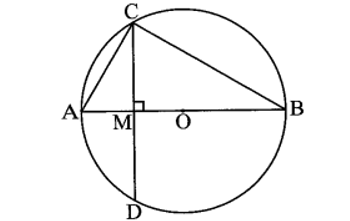
Cho đường tròn (O) đường kính AB, vẽ dây CD vuông góc với AB tại M

Cho đường tròn (O) đường kính AB, vẽ dây CD vuông góc với AB tại M. Cho biết AM = 1 cm, Tính:

Giải sách bài tập Toán 9 Bài 1: Đường tròn - Chân trời sáng tạo

Bài 5 trang 85 sách bài tập Toán 9 Tập 1: Cho đường tròn (O) đường kính AB, vẽ dây CD vuông góc với AB tại M. Cho biết AM = 1 cm, $CD=2\sqrt{3} \text{cm}.$ Tính:

a) Bán kính đường tròn (O).

b) Số đo $\widehat{CAB}.$

Lời giải:

a) Ta có đường kính AB là trục đối xứng của đường tròn (O)

Suy ra $MC=MD=\frac{CD}{2}=\frac{2\sqrt{3}}{2}=\sqrt{3} \left(\text{cm}\right).$

Tam giác ABC có CO là đường trung tuyến và $CO=\frac{1}{2}AB,$ suy ra ABC là tam giác vuông tại C.

Do $\widehat{CAM}+\widehat{CBM}=90°;\widehat{CAM}+\widehat{ACM}=90°$ nên $\widehat{CBM}=\widehat{ACM}.$

Xét ∆CMB và ∆AMC có:

$\widehat{AMC}=\widehat{CMB}=90°$ và $\widehat{CBM}=\widehat{ACM}$

Do đó ∆CMB ᔕ ∆AMC (g.g).

Suy ra $\frac{MC}{MA}=\frac{MB}{MC},$ nên $MB=\frac{M{C}^2}{MA}=\frac{{\left(\sqrt{3}\right)}^2}{1}=3 \left(\text{cm}\right).$

Gọi R là bán kính đường tròn đường kính AB, khi đó AB = 2R.

Ta có AB = MA + MB = 1 + 3 = 4 = 2R, suy ra R = 2 cm.

b) Xét tam giác AMC vuông tại M, ta có:

$\tan \widehat{CAB}=\tan \widehat{CAM}=\frac{MC}{MA}=\frac{\sqrt{3}}{1}=\sqrt{3},$ suy ra $\widehat{CAB}\approx 60°.$

Lời giải SBT Toán 9 Bài 1: Đường tròn hay khác:

• Bài 1 trang 84 sách bài tập Toán 9 Tập 1: Chứng minh bốn đỉnh của hình vuông ABCD có cạnh bằng 16 cm đều nằm trên một đường tròn. Tính bán kính của đường tròn này...

• Bài 2 trang 84 sách bài tập Toán 9 Tập 1: Cho tam giác ABC có AB = AC = 13 cm, BC = 10 cm và có BH, CK là hai đường cao. ...

• Bài 3 trang 85 sách bài tập Toán 9 Tập 1: Xác định vị trí tương đối của hai đường tròn (O; R) và (O’; R’) trong mỗi trường hợp sau:...

• Bài 4 trang 85 sách bài tập Toán 9 Tập 1: Cho đường tròn (O; 8 cm) và hai điểm A, B nằm trên đường tròn thoả mãn AB = 6 cm. Vẽ đường kính MN sao cho hai đoạn thẳng MN và AB không có điểm chung...

• Bài 6 trang 85 sách bài tập Toán 9 Tập 1: Cho hai điểm A, B trên đường tròn (O; R). Cho biết AB = 9 cm và khoảng cách từ O đến đường thẳng AB ...

• Bài 7 trang 85 sách bài tập Toán 9 Tập 1: Tìm trục đối xứng của hình tạo bởi hai đường tròn (O) và (O’) trong Hình 12....

• Bài 8 trang 85 sách bài tập Toán 9 Tập 1: Cho hình vuông ABCD có cạnh bằng 4 cm. a) Vẽ các đường tròn tâm A, B, C, D bán kính 2 cm...