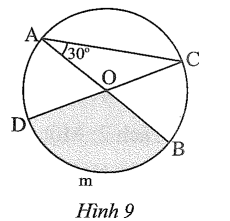
Cho đường tròn (O) đường kính AB = 3 cm, góc CAB = 30 độ (Hình 9). Tính độ dài cung BmD

Cho đường tròn (O) đường kính AB = 3 cm, (Hình 9).

Giải sách bài tập Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên - Chân trời sáng tạo

Bài 2 trang 97 sách bài tập Toán 9 Tập 1: Cho đường tròn (O) đường kính AB = 3 cm, $\hat{C A B} = 30 °$ (Hình 9).

a) Tính độ dài cung BmD.

b) Tính diện tích hình quạt tròn OBmD.

Lời giải:

a) Xét ∆OAC cân tại O (do OA = OC), suy ra $\hat{O C A} = \hat{O A C} = 30 ° .$

Lại có $\hat{O C A} + \hat{O A C} + \hat{A O C} = 180 °$

Suy ra $\hat{A O C} = 180 ° - \hat{O C A} - \hat{O A C} = 180 ° - 30 ° - 30 ° = 120 °$

Do đó $\hat{D O B} = \hat{A O C} = 120 °$ (đối đỉnh).

Do AB = 3 cm, suy ra $A O = O B = \frac{1}{2} A B = \frac{1}{2} \cdot 3 = 1, 5$ (cm).

Cung BmD có số đo 120°, bán kính R = 1,5 cm có độ dài là:

$l_{\overset{⏜}{B m D}} = \frac{π \cdot 1, 5 \cdot 120}{180} = π \approx 3, 14 (cm) .$

b) Diện tích hình quạt tròn OBmD bán kính R = 1,5 cm là:

$S_{O B m D} = \frac{π \cdot 1, 5^{2} \cdot 120}{360} = \frac{3}{4} π \approx 2, 36 ({cm}^{2}) .$

Lời giải SBT Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên hay khác: