Cho parabol (P) y = (3/2) x^2 và đường thẳng d: y = 3x. Vẽ (P) và d trên cùng một mặt phẳng toạ độ Oxy

Cho parabol và đường thẳng d: y = 3x.

Giải sách bài tập Toán 9 Bài 1: Hàm số và đồ thị của hàm số y = ax ^2 (a ≠ 0) - Chân trời sáng tạo

Bài 3 trang 7 sách bài tập Toán 9 Tập 2: Cho parabol $(P) : y = \frac{3}{2} x^{2}$ và đường thẳng d: y = 3x.

a) Vẽ (P) và d trên cùng một mặt phẳng toạ độ Oxy.

b) Dựa vào hình vẽ, tìm toạ độ giao điểm của (P) và d.

Lời giải:

a) ‒ Vẽ đồ thị hàm số $(P) : y = \frac{3}{2} x^{2}$

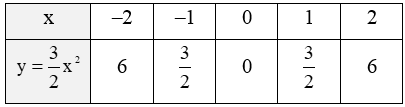
Ta có bảng giá trị của hàm số:

Cho parabol (P) y = (3/2) x^2 và đường thẳng d: y = 3x. Vẽ (P) và d trên cùng một mặt phẳng toạ độ Oxy

• Trên mặt phẳng tọa độ Oxy, lấy các điểm A(–2; 6); $B (- 1; \frac{3}{2}),$ O(0; 0); $B^{'} (1; \frac{3}{2}),$ A’(2; 6).

• Đồ thị của hàm số $y = \frac{3}{2} x^{2}$ là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như hình vẽ.

‒ Vẽ đường thẳng d: y = 3x.

Đồ thị của hàm số y = 3x là đường thẳng đi qua các điểm O(0; 0) và A’(2; 6).

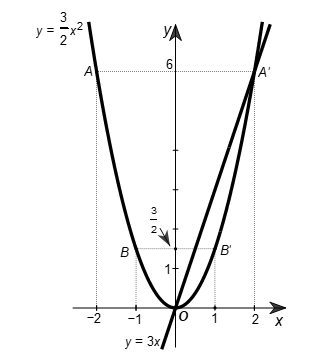
Đồ thị của hai hàm số $y = \frac{3}{2} x^{2}$ và y = 3x được vẽ như sau:

Cho parabol (P) y = (3/2) x^2 và đường thẳng d: y = 3x. Vẽ (P) và d trên cùng một mặt phẳng toạ độ Oxy

b) Dựa vào hình vẽ, ta có các giao điểm của (P) và d là O(0; 0) và A’(2; 6).

Lời giải SBT Toán 9 Bài 1: Hàm số và đồ thị của hàm số y = ax² (a ≠ 0) hay khác: