Cho đường tròn (O) và điểm P. Giả sử P thuộc O. Vẽ đường thẳng a đi qua P và vuông góc với OP
Cho đường tròn (O) và điểm P.
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn - Kết nối tri thức
Bài 5.17 trang 65 sách bài tập Toán 9 Tập 1: Cho đường tròn (O) và điểm P.
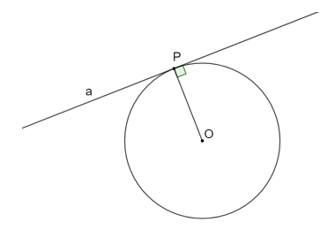
a) Giả sử . Vẽ đường thẳng a đi qua P và vuông góc với OP. Chứng minh rằng a là tiếp tuyến của đường tròn (O) tại P.
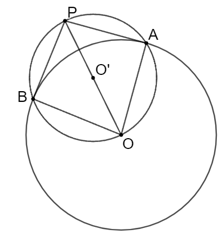
b) Giả sử P nằm ngoài (O). Vẽ đường tròn đường kính OP. Đường tròn vừa vẽ cắt (O) tại A và B. Chứng minh rằng PA và PB là hai tiếp tuyến của (O).
Lời giải:
a)
Ta có OP là bán kính đường tròn (O) (do ) và a ⊥ OP.
Do đó a là tiếp tuyến của đường tròn (O) tại P. (đpcm)
b)
Gọi đường tròn bán kính OP là đường tròn (O').
Do A nằm trên đường tròn (O') đường kính OP nên tam giác BOP vuông tại B.
Suy ra OB ⊥ BP.
Ta có: OB là bán kính đường tròn (O) và OB ⊥ BP.
Do đó BP là tiếp tuyến của đường tròn (O) tại B. (đpcm)
Tương tự ta chứng minh được PA là tiếp tuyến của đường tròn (O) tại A.
Lời giải SBT Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn hay khác: