Cho đường thẳng a, điểm M thuộc a và số dương R. Vẽ đường thẳng b đi qua M và vuông góc với a
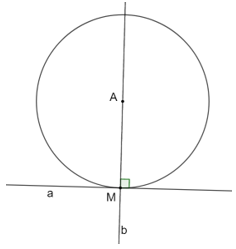
Cho đường thẳng a, điểm M thuộc a và số dương R. Vẽ đường thẳng b đi qua M và vuông góc với a. Trên b xác định điểm A sao cho AM = R (đvđd). Chứng minh rằng đường tròn (A; R) tiếp xúc với a tại M. Ta có thể vẽ được mấy đường tròn như thế?
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn - Kết nối tri thức
Bài 5.18 trang 65 sách bài tập Toán 9 Tập 1: Cho đường thẳng a, điểm M thuộc a và số dương R. Vẽ đường thẳng b đi qua M và vuông góc với a. Trên b xác định điểm A sao cho AM = R (đvđd). Chứng minh rằng đường tròn (A; R) tiếp xúc với a tại M. Ta có thể vẽ được mấy đường tròn như thế?
Lời giải:
Ta có: a ⊥ AM (do a ⊥ b và );
AM là bán kính của (A; R).
Do đó a là tiếp tuyến của (A; R) tại M hay (A; R) tiếp xúc với a tại M. (đpcm)
Có thể vẽ được hai đường tròn như thế, vì ta có thể lấy 2 điểm A nằm trên b nằm về hai phía của đường thẳng a và cách M một khoảng bằng R.
Lời giải SBT Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn hay khác: