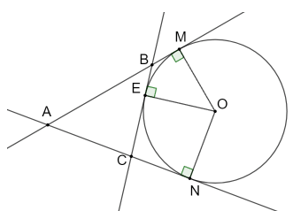
Cho AM và AN là hai tiếp tuyến cắt nhau của đường tròn (O), trong đó M và N là hai tiếp điểm
Cho AM và AN là hai tiếp tuyến cắt nhau của đường tròn (O), trong đó M và N là hai tiếp điểm. Gọi E là một điểm thuộc cung nhỏ MN. Tiếp tuyến của (O) tại E cắt AM tại B và cắt AN tại C. Biết AB = 10 cm, AC = 7 cm và BC = 6 cm. Tính độ dài của các đoạn thẳng AM, AN, BM và CN.
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn - Kết nối tri thức
Bài 5.20 trang 65 sách bài tập Toán 9 Tập 1: Cho AM và AN là hai tiếp tuyến cắt nhau của đường tròn (O), trong đó M và N là hai tiếp điểm. Gọi E là một điểm thuộc cung nhỏ MN. Tiếp tuyến của (O) tại E cắt AM tại B và cắt AN tại C. Biết AB = 10 cm, AC = 7 cm và BC = 6 cm. Tính độ dài của các đoạn thẳng AM, AN, BM và CN.
Lời giải:
Do AM và AN, BM và BE, CN và CE là các cặp tiếp tuyến cắt nhau của (O) nên ta có:
AM = AN; BM = BE; CN = CE
Suy ra AM + AN = AB + BM + AC + CN = AB + BE + AC + CE
Do đó 2AM = AB + AC + (BE + CE) = AB + AC + BC
Khi đó (cm);
AN = AM = 11,5 cm;
BM = AM – AB = 11,5 – 10 = 1,5 (cm);
CN = AN – AC = 11,5 – 7 = 4,5 (cm).
Vậy AM = AN = 11,5 cm, BM = 1,5 cm và CN = 4,5 cm.
Lời giải SBT Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn hay khác: