Cho đường thẳng a, điểm M thuộc a và số dương R. Vẽ đường thẳng b đi qua M và vuông góc với a
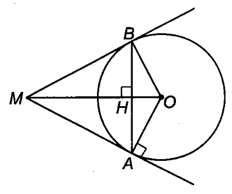
Cho đường tròn (O) và điểm M nằm bên ngoài (O). Từ M kẻ tiếp tuyến MA với (O), trong đó A là tiếp điểm. Đường thẳng qua A và vuông góc với MO cắt (O) tại B (khác A).
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn - Kết nối tri thức
Bài 5.19 trang 65 sách bài tập Toán 9 Tập 1: Cho đường tròn (O) và điểm M nằm bên ngoài (O). Từ M kẻ tiếp tuyến MA với (O), trong đó A là tiếp điểm. Đường thẳng qua A và vuông góc với MO cắt (O) tại B (khác A).
a) Chứng minh rằng MB là tiếp tuyến của (O);
b) Tính OM và diện tích phần của tam giác AMB nằm bên ngoài (O), biết bán kính của (O) bằng 3 cm và = 60°.
Lời giải:
a) Gọi H là giao điểm của MO và AB.
+ Xét hai tam giác vuông AOH và BOH có:
Chung cạnh OH; OA = OB (bán kính đường tròn (O))
Do đó ∆AOH = ∆BOH (c.g.c), suy ra , hay .
+ Xét ∆AOM và ∆BOM có:
Chung cạnh OM; ; OA = OB
Do đó ∆AOM = ∆BOM (c.g.c), suy ra hay OB ⊥ MB.
Ta có: OB ⊥ MB và OB là bán kính của đường tròn (O)
Do đó MB là tiếp tuyến của đường tròn (O). (đpcm)
b) Vì MA và MB là hai tiếp tuyến của đường tròn (O) và cắt nhau tại M nên MA = MB, suy ra tam giác MAB cân tại M. Mà nên tam giác MAB là tam giác đều.
Xét tứ giác AOBM ta có:
Suy ra
Do đó số đo cung nhỏ AB là sđ .
Diện tích hình quạt ứng với cung nhỏ AB là:
(cm2)
Ta có (tính chất hai tiếp tuyến cắt nhau)
Xét tam giác AOM vuông tại A, ta có:
(cm)
Theo câu a, ∆AOM = ∆BOM nên ta có:
(cm2)
Diện tích phần tam giác AMB nằm bên ngoài đường tròn (O) là:
(cm2)
Áp dụng định lý Pythagore với tam giác AOM ta được:
(cm).
Vậy OM = 6 cm và diện tích phần tam giác AMB nằm bên ngoài đường tròn (O) là cm2.
Lời giải SBT Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn hay khác: