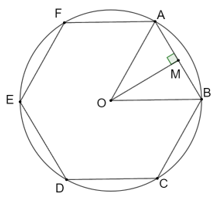
Cho lục giác đều ABCDE nội tiếp một đường tròn (O). Chứng minh rằng điểm O cách đều tất cả các cạnh của lục giác đều
Cho lục giác đều ABCDE nội tiếp một đường tròn (O). Chứng minh rằng điểm O cách đều tất cả các cạnh của lục giác đều.
Giải sách bài tập Toán 9 Bài 30: Đa giác đều - Kết nối tri thức
Bài 9.36 trang 60 sách bài tập Toán 9 Tập 2: Cho lục giác đều ABCDE nội tiếp một đường tròn (O). Chứng minh rằng điểm O cách đều tất cả các cạnh của lục giác đều.
Lời giải:
Gọi a là độ dài cạnh của lục giác đều ABCDEF.
Gọi M là trung điểm của AB.
Vì tam giác AOB là tam giác đều nên OM ⊥ AB và OM là phân giác của góc AOB.
Do đó
Vậy khoảng cách từ điểm O đến AB bằng
Tương tự ta tính được khoảng cách từ O đến tất cả các cạnh của lục giác đều đều bằng nhau và bằng
Vậy điểm O cách đều tất cả các cạnh của lục giác đều.
Lời giải SBT Toán 9 Bài 30: Đa giác đều hay khác:
Bài 9.33 trang 59 sách bài tập Toán 9 Tập 2: Những hình nào dưới đây là đa giác đều? ...
Bài 9.34 trang 59 sách bài tập Toán 9 Tập 2: Hình phẳng nào dưới đây có dạng đa giác đều? ...